Непрерывные случайные величины. Плотность вероятности

Функцией распределения случайной величины Х называется функция F (х), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х: .

Функцию F (х) иногда называют интегральной функцией распределения, или интегральным законом распределения.

Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Примеры непрерывных случайных величин: диаметр детали, которую токарь обтачивает до заданного размера, рост человека, дальность полета снаряда и др.

Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю

.

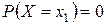Следствие. Если Х — непрерывная случайная величина, то вероятность попадания случайной величины в интервал не зависит от того, является этот интервал открытым или закрытым, т.е.

.

Если непрерывная случайная величина Х может принимать только значения в границах от а до b (где а и b — некоторые постоянные), то функция распределения ее равна нулю для всех значений и единице для значений .