 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Непрерывность функции. Ситуация с вычислением предела сложной функции упрощается, если рассматривать функции, для которых возможен непосредственный предельный переход .
|
|
Ситуация с вычислением предела сложной функции упрощается, если рассматривать функции, для которых возможен непосредственный предельный переход  .
.
Такие функции получили название непрерывных. Функция 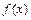 называется непрерывной в точке
называется непрерывной в точке  , если предел
, если предел
 .
.
Это условие допускает эквивалентную формулировку «на языке  »:
»:
 .
.
Если обозначить  ,
,  , то определение предела можно сформулировать через приращения:
, то определение предела можно сформулировать через приращения:
 .
.
Точка, в которой функция не является непрерывной, называется точкой разрыва. Для классификации точек разрыва пользуются определением непрерывности через односторонние пределы. Функция 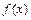 называется непрерывной в точке
называется непрерывной в точке  , если
, если
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
Функция 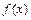 имеет в точке
имеет в точке  устранимый разрыв, если выполняются условия 1)-3), но не выполняется условие 4), т.е. точка
устранимый разрыв, если выполняются условия 1)-3), но не выполняется условие 4), т.е. точка  , либо односторонние пределы не равны
, либо односторонние пределы не равны  .
.
Функция 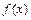 имеет в точке
имеет в точке  разрыв I рода (разрыв скачка), если выполняются условия 1)-2), но не выполняется условие 3), т.е. существуют конечные односторонние пределы, но они различны.
разрыв I рода (разрыв скачка), если выполняются условия 1)-2), но не выполняется условие 3), т.е. существуют конечные односторонние пределы, но они различны.
Функция 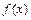 имеет в точке
имеет в точке  разрыв II рода, если не существует или равен бесконечности по крайней мере один из односторонних пределов.
разрыв II рода, если не существует или равен бесконечности по крайней мере один из односторонних пределов.
Функция 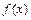 называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Теорема. Все элементарные функции непрерывны в своей области определения.
Теорема (Коши о промежуточных значениях функции, непрерывной на отрезке). Если функция непрерывна на отрезке  и
и  ,
,  , то для любого числа C, заключенного между A и B, существует точка
, то для любого числа C, заключенного между A и B, существует точка  , в которой значение
, в которой значение  .
.
Теорема (Вейерштрасса об ограниченности функции, непрерывной на отрезке). Если функция непрерывна на отрезке, то она ограничена на нем.
Теорема (Вейерштрасса о достижении наибольшего и наименьшего значений функции, непрерывной на отрезке). Если функция непрерывна на отрезке, то среди её значений на этом отрезке есть наибольшее и наименьшее.
Функция 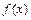 называется равномерно непрерывной на множестве E, если она определена на этом множестве и
называется равномерно непрерывной на множестве E, если она определена на этом множестве и
 .
.
Всякая равномерно непрерывная на множестве E функция является непрерывной на этом множестве.
Пример. Функция  , непрерывна, но не равномерно непрерывна на интервале
, непрерывна, но не равномерно непрерывна на интервале  .
.
Теорема (Кантор). Если функция непрерывна на отрезке, то она равномерно непрерывна на этом отрезке.
Задача 19. Исследовать на непрерывность и построить эскиз графика функции

в окрестности точки  .
.
Решение. Найдем односторонние пределы функции в точке  . Левосторонний предел
. Левосторонний предел
 .
.
Правосторонний предел
 .
.
Следовательно, в точке  не существует предела и функция разрывна. Эскиз графика функции в окрестности точки
не существует предела и функция разрывна. Эскиз графика функции в окрестности точки  будет иметь вид
будет иметь вид

Рис. 20
Можно этим и ограничиться. Но в данном случае не очень сложно установить поведение функции и вне окрестности точки  . Так, например, справа от начала координат функция монотонно убывает, оставаясь положительной. Вычислим предел
. Так, например, справа от начала координат функция монотонно убывает, оставаясь положительной. Вычислим предел
 .
.
Это означает, что график функции неограниченно приближается к положительной полуоси OX сверху.
Для отрицательных аргументов из условия  следует, что
следует, что
 ,
,
так как знаменатель дроби – положительная величина (произведение двух неотрицательных величин), а числитель – отрицательная (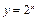 - возрастающая функция). Таким образом, при
- возрастающая функция). Таким образом, при  функция монотонно убывает.
функция монотонно убывает.
Предел  . Это означает, что при
. Это означает, что при  график функции неограниченно приближается к прямой
график функции неограниченно приближается к прямой  . Таким образом, эскиз графика будет иметь вид
. Таким образом, эскиз графика будет иметь вид

Рис. 21
Задача 20. Функция  не определена при
не определена при 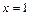 . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке 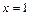 она стала непрерывной?
она стала непрерывной?
Решение. Речь идет о существовании новой функции, общей с данной функцией во всех точках, кроме точки 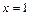 , и непрерывной в этой точке. Это зависит от того, существует ли придел данной функции в точке
, и непрерывной в этой точке. Это зависит от того, существует ли придел данной функции в точке 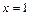 . Имеем
. Имеем

 .
.
Так как предел существует, то доопределить заданную функцию в точке 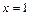 по непрерывности можно. В результате получим функцию
по непрерывности можно. В результате получим функцию
 .
.
Задача 21. Доказать, что уравнение 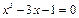 имеет, по крайней мере, один действительный корень, заключенный между 1 и 2.
имеет, по крайней мере, один действительный корень, заключенный между 1 и 2.
Решение. Рассмотрим функцию  и покажем, что она на отрезке
и покажем, что она на отрезке  удовлетворяет условиям теоремы Коши-Больцано: «Если функция непрерывна на отрезке
удовлетворяет условиям теоремы Коши-Больцано: «Если функция непрерывна на отрезке  и на концах этого отрезке принимает значения разных знаков, то между точками a и b найдется точка c, в которой
и на концах этого отрезке принимает значения разных знаков, то между точками a и b найдется точка c, в которой  ».
».
Данная функция непрерывна на отрезке  как многочлен, значения
как многочлен, значения  и
и  . На основании сформулированной теоремы найдется точка c, в которой
. На основании сформулированной теоремы найдется точка c, в которой  . Эта точка принадлежит интервалу (1; 2) и является корнем уравнения
. Эта точка принадлежит интервалу (1; 2) и является корнем уравнения 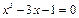 .
.
Задания для самостоятельной работы
Вариант № 1
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения:
а)  ; б)
; б)  ; в)
; в)  .
.
4. Решить неравенства:
а)  ; б)
; б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г) 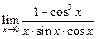 ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Пользуясь определением предела, доказать, что
а)  ; б)
; б)  .
.
7. Исследовать на непрерывность и построить эскиз графика функции  в окрестности точки
в окрестности точки  .
.
8. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
9. Доказать, что функция  на отрезке
на отрезке 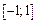 принимает значение, равное 4.
принимает значение, равное 4.
Вариант № 2
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения:
а)  ; б)
; б)  ; в)
; в)  .
.
4. Решить неравенства:
а)  б)
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  в окрестности точки
в окрестности точки  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б) 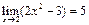 .
.
9. Функция 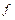 , определенная на
, определенная на  , принимает все промежуточные значения между
, принимает все промежуточные значения между  и
и  . Достаточно ли этого для непрерывности
. Достаточно ли этого для непрерывности 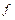 на
на  ?
?
Вариант № 3
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б) 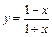 .
.
3. Решить уравнения:
а) 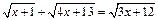 ; б)
; б)  ;
;
в)  .
.
4. Решить неравенства:
а)  ; б)
; б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции 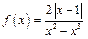 при
при  и
и  ,
, 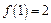 ,
,  в окрестности точек
в окрестности точек  и
и 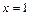 .
.
7. Функция 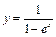 не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Функция 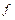 определена на
определена на  и ни в одной точке
и ни в одной точке  не принимает значения
не принимает значения  . Следует ли отсюда, что
. Следует ли отсюда, что 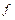 – разрывна?
– разрывна?
Вариант № 4
1. Найти естественную область определения функции:
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б) 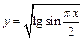 .
.
3. Решить уравнения:
а)  ; б)
; б)  ;
;
в)  .
.
4. Решить неравенства:
а)  ; б)
; б)  ; в)
; в)  .
.
4. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  в окрестностях точек
в окрестностях точек  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а) 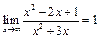 ; б)
; б)  .
.
9. Доказать, что для любого многоугольника существует прямая, делящая его на равновеликие части.
Вариант № 5
1. Найти естественную область определения функции
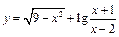 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
4. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  .
.
7. Функция  не определена при
не определена при 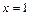 . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке 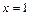 она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Можно ли утверждать, что если функция 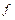 определена на отрезке
определена на отрезке  и непрерывна на интервале
и непрерывна на интервале  , то она будет ограничена на
, то она будет ограничена на  ?
?
Вариант № 6
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а) 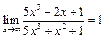 ; б)
; б)  .
.
9. Могут ли все значения функции, непрерывной на интервале  образовать отрезок?
образовать отрезок?
Вариант № 7
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а) 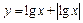 ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в) 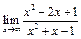 ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Показать, что уравнение  имеет на отрезке
имеет на отрезке  корень.
корень.
Вариант № 8
1. Найти естественную область определения функции:
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д) 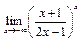 ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Доказать, что всякий многочлен нечетной степени имеет по крайней мере один действительный корень.
Вариант № 9
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а) 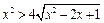 ;
;
б) 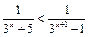 ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Найти и исследовать точки разрыва функции  , равной
, равной  , если
, если 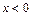 ; равной
; равной  , если
, если  ; равной 3, если
; равной 3, если  .
.
Вариант № 10
1. Найти естественную область определения функции
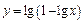 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а) 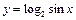 ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в) 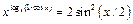 .
.
4. Решить неравенства: а) 
 ;
;
 б)
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  в окрестности точки
в окрестности точки  .
.
7. Функция  не определена при
не определена при 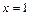 . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке 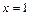 она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9.Найти и исследовать точки разрыва функции
 .
.
Вариант № 11
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
 б)
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  ,
,  ,
,  в окрестности точки
в окрестности точки  .
.
7. Функция  не определена при
не определена при 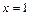 . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке 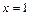 она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б) 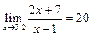 .
.
9. Найти и исследовать точки разрыва функции
 .
.
Вариант № 12
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить эскиз графика функции  в окрестности точки
в окрестности точки  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Привести пример, показывающий, что сумма двух разрывных функций может быть функцией непрерывной. Что можно сказать о непрерывности суммы разрывной и непрерывной функции?
Вариант № 13
1. Найти естественную область определения функции
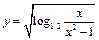 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а) 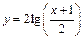 ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б) 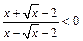 ; в)
; в)  .
.
5. Вычислить пределы
а)  ; г)
; г) 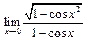 ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить график функции
 .
.
7. Функция  не определена при
не определена при 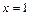 . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке 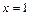 она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9.Пусть  . Доказать, что
. Доказать, что 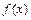 всюду разрывна.
всюду разрывна.
Вариант № 14
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а) 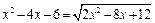 ;
;
б) 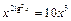 ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
 б)
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б) 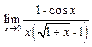 ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить график функции  в окрестности точки
в окрестности точки  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9. Можно ли привести пример двух различных функций, непрерывных на  и совпадающих на множестве всех рациональных чисел из
и совпадающих на множестве всех рациональных чисел из  ?
?
Вариант № 15
1. Найти естественную область определения функции:
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
 б)
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а) 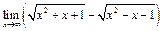 ; г)
; г)  ;
;
б)  ; д)
; д)  .
.
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить график функции  в окрестности точки
в окрестности точки  .
.
7. Функция 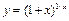 не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9.Доказать, что если функция 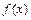 непрерывна в точке
непрерывна в точке  , то она ограничена в некоторой окрестности этой точки. Верно ли обратное утверждение?
, то она ограничена в некоторой окрестности этой точки. Верно ли обратное утверждение?
Вариант № 16
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить график функции 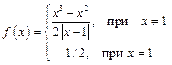 в окрестности точки
в окрестности точки 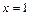 .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9.Доказать существование обратной функции для  ,
,  . Указать область определения обратной функции.
. Указать область определения обратной функции.
Вариант № 17
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а) 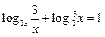 ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а)  ;
;
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а)  ; г)
; г)  ;
;
б) 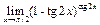 ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить график функции  в окрестности точки
в окрестности точки  .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б)  .
.
9.Имеет ли уравнение  корни, принадлежащие интервалу
корни, принадлежащие интервалу  ?
?
Вариант № 18
1. Найти естественную область определения функции
 .
.
2. Используя графики основных элементарных функций и методы преобразования функций, построить графики функций:
а)  ; б)
; б)  .
.
3. Решить уравнения: а)  ;
;
б)  ; в)
; в)  .
.
4. Решить неравенства: а) 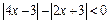 ;
;
 б)
б)  ; в)
; в)  .
.
5. Вычислить пределы:
а) 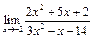 ; г)
; г) 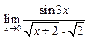 ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
6. Исследовать на непрерывность и построить графика функции
 .
.
7. Функция  не определена при
не определена при  . Можно ли ее доопределить так, чтобы в точке
. Можно ли ее доопределить так, чтобы в точке  она стала непрерывной?
она стала непрерывной?
8. Пользуясь определением предела, доказать:
а)  ; б)
; б) 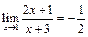 .
.
Дата публикования: 2014-10-20; Прочитано: 905 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
