Вычисление пределов

Пусть 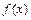- основная элементарная функция. Тогда для любого предел

, (1)

т.е. для основных элементарных функций можно осуществлять непосредственный предельный переход (1).

При построении элементарных функций используются операции перехода 1 - 5. Для основных элементарных функций предельный переход выдерживается относительно этих операций. Именно, пусть 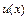и - основные элементарные функции, и существуют конечные пределы и . Тогда выполняются следующие свойства предела:

1) ;

2) ;

3) ;

4) , если .

Пусть 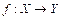и - основные элементарные функции, и существуют конечные пределы и 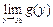. Тогда

5) .

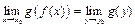Эти свойства выполняются и для элементарных функций, что позволяет распространить непосредственный предельный переход на класс элементарных функций.

Если функции неэлементарные, то предельный переход будет выдерживаться только относительно арифметических операций, а операция образования сложной функции может нарушить этот предельный переход. Например, для функций , и

для любого имеем , , и .

Для любых функций справедливы более слабые, чем свойство 5), утверждения

.

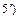
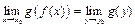, если в некоторой проколотой окрестности точки .

Часто рассматриваются случаи, когда предельная точка не принадлежит области определения функции. Например, встречаются выражения и . В результате непосредственного предельного перехода могут получаться так называемые неопределенности, например, 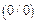, , , и т.д. Для раскрытия неопределенностей нужно применять тождественные преобразования, различные оценки или замечательные пределы:

1- й замечательный предел ;

2- й замечательный предел .

Следствия из второго замечательного предела:

, ,

, , .

Функции и называются эквивалентными при , если .

Задача 13. Вычислить предел .

Решение. Непосредственный предельный переход приводит к неопределенности 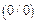. Для ее раскрытия необходимо и числитель и знаменатель дроби разложить на множители и произвести сокращение. При этом один из множителей должен быть . Это подсказывает нам способ группировки слагаемых для разложения многочленов на множители:

.

Теперь можно воспользоваться свойством предела частного функций:

.

Ответ: -9.

Задача 14. Вычислить предел .

Решение. Непосредственный предельный переход приводит к неопределенности . Для ее раскрытия умножим и одновременно разделим выражение, стоящее под знаком предела, на сопряженное выражение . Получим

.

Теперь имеется неопределенность вида . Для ее раскрытия разделим числитель и знаменатель дроби на :

.

Ответ: 1.

Задача 15. Вычислить предел .

Решение. Непосредственный предельный переход приводит к неопределенности . Для ее раскрытия нужно упростить тригонометрическое выражение, сведя функцию к единому аргументу по формулам

.

В результате получим

.

Так как , то и после сокращения получаем

.

Ответ: .

Задача 16. Вычислить предел .

Решение. Непосредственный предельный переход приводит к неопределенности 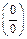. Для ее раскрытия домножим числитель и знаменатель на сопряженное выражение . Получим

.

Ответ: 1.

Задача 17. Вычислить предел .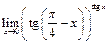

Решение. Непосредственный предельный переход приводит к неопределенности . Для ее раскрытия приведем выражение к стандартному для 2-го замечательного предела виду:

.

Ответ: .

Задача 18. Вычислить предел .

Решение. Непосредственный предельный переход приводит к неопределенности . Для ее раскрытия приведем выражение к стандартному для 2-го замечательного предела виду:

.

Ответ: .