Множество действительных чисел

Для числовых множеств общеприняты следующие обозначения:

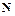- множество натуральных чисел,

- множество целых чисел,

- множество рациональных чисел,

- множество действительных чисел.

Кроме этого, часто употребляются знаки:

- для любого,

- существует,

- равно по определению.

Действительные числа вводятся аксиоматически: - множество, для которого выполняются

1) аксиомы сложения;

2) аксиомы умножения;

3) дистрибутивность умножения относительно сложения;

4) аксиомы порядка;

5) аксиома непрерывности.

Первые четыре группы аксиом подробно рассматриваются в курсе алгебры.

Аксиома непрерывности действительных чисел. Если A и B – непустые подмножества множества действительных чисел такие, что для любых элементов и выполняется неравенство , то существует такой элемент , что для любых элементов и выполняется неравенство .

Аксиома непрерывности, в частности, позволяет установить взаимно однозначное соответствие между множеством действительных чисел и точками числовой оси.

Множество называется ограниченным снизу, если

(число называется нижней гранью множества ).

Множество называется ограниченным сверху, если

(число называется верхней гранью множества ).

Множество E называется ограниченным, если оно ограничено и снизу и сверху.

Число m называется точной нижней гранью множества E, пишут , если

1) ;

2) .

Число M называется точной верхней гранью множества E, пишут , если

1) ;

2) .

Число m называется наименьшим элементом множества E, пишут , если

1) ;

2) .

Число M называется наибольшим элементом множества E, пишут , если

1) ;

2) .

Пример. Рассмотрим множество . Наименьшего элемента нет, , .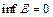

Множество действительных чисел обладает свойством полноты, которое выражается следующим предложением.

Теорема. Всякое непустое ограниченное сверху множество имеет точную верхнюю грань. (Всякое непустое ограниченное снизу множество имеет точную нижнюю грань.)

Принцип математической индукции. Утверждение считается верным для любого , если

1) - верно;

2) из предположения, что - верно, следует верность .

По принципу математической индукции можно доказать, например, неравенство Бернулли

.

Абсолютной величиной (или модулем) действительного числа называется

.

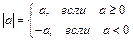Модуль числа – это расстояние соответствующей точки до нуля на числовой оси, модуль разности двух чисел – это расстояние между соответствующими точками числовой оси. Свойства модуля:

1) ;

2) ;

3) эквивалентно ;

4) ;

5) .

Расширенное множество действительных чисел 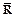– это множество действительных чисел, дополненное двумя символами . Под символом понимают или .

Система отрезков называется вложенной, если

Теорема (Кантор). Для всякой системы вложенных отрезков существует хотя бы одно действительное число, принадлежащее всем отрезкам системы.

Система вложенных отрезков называется стягивающейся, если длины отрезков стремятся к нулю:

.

Теорема. Для всякой стягивающейся системы вложенных отрезков существует единственная общая точка.