 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства. Термин фрактал был предложен Бенуа Мандельбротом (B
|
|
- Отображение соленоида гиперболично.
- Сам соленоид оказывается гомеоморфен множеству, получаемому при реализации процедуры надстройки над одометром — отображением прибавления единицы в 2-адических целых числах
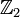 .
. - Динамика на соленоиде допускает символическое кодирование: точке соленоида можно (почти взаимно-однозначно) сопоставить двусторонне-бесконечным последовательностям нулей и единиц, причём применению отображения будет соответствовать левый сдвиг на пространстве последовательностей, а часть последовательности с положительными индексами будет являться двоичной записью угловой координаты.
Термин фрактал был предложен Бенуа Мандельбротом (B. Mandelbrot) в 1975 году для обозначения нерегулярных самоподобных математических структур. Основное определение фрактала, данное Мандельбротом, звучало так: "Фракталом называется структура, которая состоит из частей, которые в каком-то смысле подобны целому" [37]. Следует признать, что это определение, ввиду своей нестрогости, не всегда верно. Можно привести много примеров самоподобных объектов, не являющихся фракталами, например, сходящиеся к горизонту железнодорожные пути.
В самом простом случае небольшая часть фрактала содержит информацию обо всем фрактале. Строгое определение самоподобных множеств было дано Дж. Хатчинсоном (J. Hutchinson) в 1981 году. Он назвал множество самоподобным, если оно состоит из нескольких компонент, подобных всему этому множеству, т.е. компонент получаемых афинными преобразованиями - поворотом, сжатием и отражением исходного множества.
Однако самоподобие – это хотя и необходимое, но далеко не достаточное свойство фракталов. Ведь нельзя же, в самом деле, считать фракталом точку, или плоскость, расчерченную клетками. Главная особенность фрактальных объектов состоит в том, что для их описания недостаточно «стандартной» топологической размерности 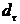 , которая, как известно, для линии равна 1 (
, которая, как известно, для линии равна 1 ( 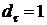 - линия одномерный объект), для поверхности
- линия одномерный объект), для поверхности 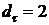 , и т.д. Фракталам характерна геометрическая «изрезанность». Поэтому используется специальное понятие фрактальной размерности, введенное Ф. Хаусдорфом (F. Hausdorf) и А.С. Безиковичем. Применительно к идеальным объектам классической евклидовой геометрии она давала те же численные значения, что и топологическая размерность, однако новая размерность обладала более тонкой чувствительностью ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо. Размерность Хаусдорфа - Безиковича как раз и позволяет измерять степень «изрезанности». Размерность фрактальных объектов не является целым числом, характерным для привычных геометрических. Вместе с тем, в большинстве случаев фракталы напоминают объекты, плотно занимающие реальное пространство, но не использующие его полностью.
, и т.д. Фракталам характерна геометрическая «изрезанность». Поэтому используется специальное понятие фрактальной размерности, введенное Ф. Хаусдорфом (F. Hausdorf) и А.С. Безиковичем. Применительно к идеальным объектам классической евклидовой геометрии она давала те же численные значения, что и топологическая размерность, однако новая размерность обладала более тонкой чувствительностью ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо. Размерность Хаусдорфа - Безиковича как раз и позволяет измерять степень «изрезанности». Размерность фрактальных объектов не является целым числом, характерным для привычных геометрических. Вместе с тем, в большинстве случаев фракталы напоминают объекты, плотно занимающие реальное пространство, но не использующие его полностью.
Пусть есть множество 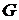 в евклидовом пространстве размерности
в евклидовом пространстве размерности 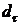 . Это множество покрывается кубиками размерности
. Это множество покрывается кубиками размерности 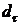 , при этом длина ребра любого кубика не превышает некоторого значения
, при этом длина ребра любого кубика не превышает некоторого значения 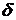 , т.е.
, т.е. 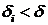 .
.
Вводится зависящая от некоторого параметра 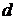 и
и 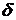 сумма по всем элементам покрытия:
сумма по всем элементам покрытия:
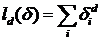 .
.
Определим нижнюю грань данной суммы:
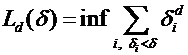 .
.
При уменьшении максимальной длины 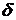 , если параметр
, если параметр 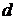 будет достаточно велик, очевидно, будет выполняться:
будет достаточно велик, очевидно, будет выполняться:
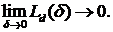
При некотором достаточно малом значении параметра 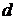 будет выполняться:
будет выполняться:
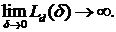
Промежуточное, критическое значение 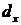 , для которого выполняется:
, для которого выполняется:
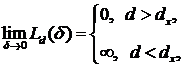
и называется размерностью Хаусдорфа-Безиковича (или фрактальной размерностью). Для простых геометрических объектов размерность Хаусдорфа-Безиковича совпадает с топологической (для отрезка 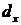 =1, для квадрата
=1, для квадрата 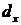 =2, для куба
=2, для куба 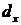 =3 и т.д.)
=3 и т.д.)
Несмотря на то, что размерность Хаусдорфа-Безиковича с теоретической точки зрения определена безупречно, для реальных фрактальных объектов расчет этой размерности является весьма затруднительным. Поэтому вводится несколько упрощенный показатель - емкостная размерность 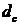 . При определении этой размерности используются кубики с гранями одинакового размера. В этом случае, естественно, справедливо:
. При определении этой размерности используются кубики с гранями одинакового размера. В этом случае, естественно, справедливо:
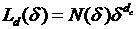 ,
,
где 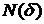 - количество кубиков, покрывающего область
- количество кубиков, покрывающего область 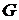 . Путем логарифмирования и перехода к пределу при уменьшении грани кубика (
. Путем логарифмирования и перехода к пределу при уменьшении грани кубика ( 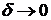 ) получаем:
) получаем:
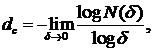
если этот предел существует. Следует отметить, что в большинстве численных методов определения фрактальной размерности используется именно 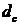 , при этом необходимо учитывать, что всегда справедливо условие:
, при этом необходимо учитывать, что всегда справедливо условие: 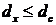 . Для регулярных самоподобных фракталов емкостная размерность и размерность Хаусдорфа-Безиковича совпадают, поэтому терминологически их часто не различают и говорят просто о фрактальной размерности объекта [13].
. Для регулярных самоподобных фракталов емкостная размерность и размерность Хаусдорфа-Безиковича совпадают, поэтому терминологически их часто не различают и говорят просто о фрактальной размерности объекта [13].
При проведении практических вычислений фрактальной размерности для реальных объектов используют следующий методический прием. Пусть на некотором этапе покрытия фрактала пришлось использовать 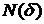 кубиков с гранями размера
кубиков с гранями размера 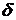 , а на другом –
, а на другом – 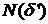 элементов с гранями размера
элементов с гранями размера 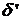 . Ввиду предполагаемой степенной зависимости справедливо:
. Ввиду предполагаемой степенной зависимости справедливо:
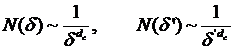 ,
,
откуда значение 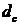 может оцениваться как:
может оцениваться как:
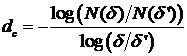 .
.
Дата публикования: 2014-10-19; Прочитано: 649 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
