Моделирование инвестиций и анализ их эффективности

С математической точки зрения, в данном случае можно использовать несколько методов:

1. метод дерева решений, метод графа решений;

2. метод статистических испытаний Монте-Карло, т.е. эта модель имитационно-статистическая.

При составлении и разработке инвестиционного проекта необходимо оценить два основных его параметра, которые взаимосвязаны. Это эффективность и риск. В качестве эффективности можно использовать так называемый NPV – чистый приведенный продукт. Существует такое понятие как опасность, а ее количественная мера – это риск. Таким образом, под риском следует понимать вероятность неблагоприятного исхода. Можно использовать коэффициент вариации, т.е. правило трех сигм. Обычно чем эффективнее проект, тем больше риск.

Рассмотрим первую модель немного подробнее. Она имеет следующие стадии:

1. прединвестиционные исследования или бизнес план. Возможные исходы:

· решение о продолжении проекта;

· решение об остановке проекта.

2. техническая реализация проекта – создание опытного образца. Возможные исходы:

· отказ от продолжения проекта (например, обнаружено, что затраты большие или выявлены технические сложности);

· реализация, требующая увеличения сроков или затрат;

· реализация в соответствии с техническим заданием.

3. техническая подготовка производства. Возможные исходы:

· невозможность производства серийного продукта;

· подготовка производства;

· выпуск инвестиционного продукта.

4. производство инвестиционного продукта. Возможные исходы:

· производство завершается выпуском первой партии (первого образца), в связи с отказом потребителя от товара;

· производство различными объемами.

5. эксплуатация (использование) инвестиционного продукта.

Эти стадии можно представить в виде ребер графа, а исходы – в виде вершин. На ребрах могут указываться оценки вероятности того или иного исхода. Следует помнить, что сумма вероятностей должна равняться 1.

С помощью графа можно оценить средневзвешенную эффективность проекта, где веса – это вероятности исходов. Интегральный эффект Э_инт, средний взвешенный по вероятностям отдельных решений, будет равен:

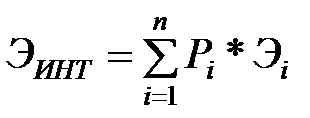
где Э_i – эффект i -го исхода;

Р_i – вероятность i -го исхода.

В качестве показателя оценки эффективности рассмотрим суммарный финансовый поток, который состоит из:

· положительного финансового потока;

· отрицательного финансового потока.

Граф следует представлять в виде динамической инвестиционной модели, т.е. учитывать процесс во времени, т.к. деньги изменяют свою стоимость. Имитируется вложение денег в банк.

Рассмотрим подход, связанный с NPV, который учитывает изменение стоимости денег при помощи дисконтирования. В качестве дисконта используется величина: 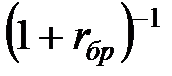, где r_бр – безрисковая ставка. Т.к. мы не получаем доход от банковских процентов, то деньги уменьшаются, т.е.

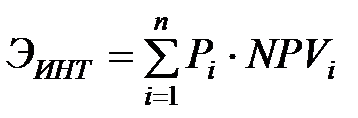, где i – номер исхода,

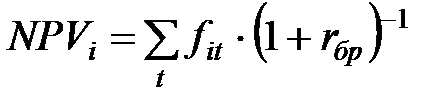, иначе это называется ожидаемый показатель.

Далее нужно сравнить ожидаемый показатель с затратами, где сумма всех отрицательных потоков – это сумма на всех этапах, кроме последнего.

При таком подходе риск оценить сложно.

Рассмотрим вторую модель – метод испытаний Монте-Карло. Его суть состоит в том, что объект можно представить в виде серого ящика, имеющим входные параметры и один или несколько выходных параметров. Нам известен алгоритм преобразования входов и выходов, но, зная значения входных параметров, аналитически определить выходные параметры нельзя. Здесь используется метод статистических испытаний. Предположим, что входные параметры заданы в виде распределения. Случайный характер могут носить затраты на разных стадиях: затраты на разработку, реализацию, производство. Отсюда можно оценить закон распределения. Кроме того, при эксплуатации инвестиционного проекта случайными величинами могут быть также цены и спрос, т.е. объемы продаж тоже, что также можно представить их законами распределения.

Далее проводится ряд опытов. Чем их больше, тем точнее получится модель (900, 1000…). В каждом эксперименте при помощи датчика случайных чисел мы получаем конкретные значения – показатели на входе. Зная алгоритм преобразования входа и выхода, находим выход. В нашем случае выход – NPV.

Р     а   ха х F*(x) – интегральный закон распределения

Получается статистическая совокупность, обработав которую, мы можем найти параметры заданной функции у и получить закон распределения у. Основное применение этот метод нашел в моделях массового обслуживания и имитационных моделях.

Каждому опыту соответствует определенное значение NPV. Затем следует упорядочить полученные значения, построить интервальный ряд и гистограмму. По ней можно подобрать уже теоретический закон распределения, который позволяет определить, какие критерии используются для непараметрических гипотез.

Имитационная модель учитывает также взаи­мосвязи некоторых переменных, основанные на закономерностях рынка. В частности:

1. Взаимосвязь цены и объемов продаж (Q(P)):

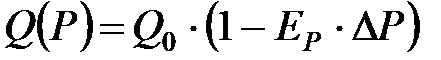
где Q₀ –объем продаж инвестиционного про­дукта, соответствующий математическое ожиданию цены (Ц₀),

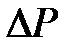– относительное изменение цены;

E_p – коэффициент эластичности спроса на инвестиционный продукт по цене. (Для систем регулирования подачи тепловой энергии принято E_p =2)

2. Зависимость издержек от объемов производства:

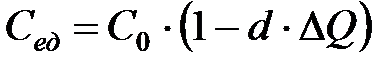
где 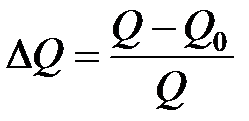– относительное изменение объема продаж;

d – постоянный коэффициент, зависящий от структуры издержек.

В данной модели можно также оценить следующие характеристики совокупности: среднее значение, показатели вариации, средне квадратическое отклонение, квантили. Также можно оценить каким-либо образом риск – это соотношение среднего значения и среднеквадратического отклонения, т.е. показателей вариации. В нашем случае риск – это отрицательное значение NPV.

Достоинством этой модели является – более полная информация, а первой – простота.