 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Модели многокритериальной оптимизации
|
|
В процессе принятия решений одним из составляющих является выбор альтернатив или вариантов. При выборе альтернатив используют различные языки. Наиболее распространенным является критериальный язык выбора альтернатив, который заключается в том, что каждой альтернативе ставится в соответствие некоторое число. Есть множество X альтернатив, где xj, 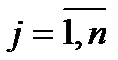 – различные альтернативы.
– различные альтернативы.
Каждой альтернативе ставится в соответствие Q(xj). Оптимальное значение может определяться как максимальное значение критерия:
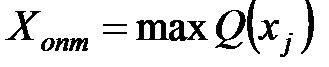
Кроме критериального языка существует язык бинарных отношений. Но в основном пользуются критеральным языком выбора: Q(xi), 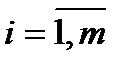 , где i – номер критерия.
, где i – номер критерия.
Случаи использования моделей многокритериальной оптимизации:
1. Система, являющаяся объектом рассмотрения, характеризуется критерием набора параметров, часть из которых противоречивы.
2. Имеется один глобальный критерий С, как правило неколичественный, сравнение и выбор альтернатив по которому затруднено. Вследствие чего происходит декомпозиция глобального критерия на локальный, по которому сравниваются альтернативы. Этот случай используется на макроэкономическом уровне.
3. При кооперативном принятии решений имеет место добровольное взаимоотношение субъектов, когда они договариваются.
Основные подходы:
1. группа методов, связанных с выдвижением аксиом ведущим функциям полезности, а аксиома проверяется лицами, принимающими решение;
2. группа методов, при использовании которых руководители непосредственно назначают вид зависимости по оценкам между различными критериями;
3. методы поэтапного определения компромисса между оценками различных критериев;
4. методы сравнения альтернатив с использованием порогов несравнимости;
5. человеко-машинные методы принятия решений по поиску лучшей альтернативы.
Вторая классификация выделяет следующие группы методов:
1. лексикографическое упорядочивание;
2. сравнение разностей критериальных оценок;
3. метод идеальной точки;
4. методы эффективность-стоимость;
5. методы свертки на иерархии критериев;
6. методы порогов независимости;
7. методы кривых безразличия;
8. методы анализа иерархий;
9. методы теории нечетких множеств;
10. методы теории ожидаемой полезности.
Третья классификация:
1. принцип равномерности;
2. принцип абсолютной уступки;
3. принцип относительной уступки;
4. принцип выделения главного критерия;
5. принцип последовательной уступки.
На основе сравнительного анализа различных подходов может быть предложена следующая классификация методов многокритериальной оптимизации:
1. Выделение множества Парето. Метод заключается в попарном сравнении альтернатив на основе выбранного бинарного отношения (например, отношения доминирования). Причем альтернативы, не худшие по всем критериям, выделяются в множество, называемым ядром. Если бинарное отношение является таким, при котором одна альтернатива имеет по всем критериям не худшие, а хотя бы по одному, лучшие оценки, то выделенное ядро называется множеством Парето.
2. Условная оптимизация. Метод основан на предположении, что можно выделить один главный критерий, а остальные использовать как ограничения. Тогда задача выбора оптимального варианта формулируется как задача нахождения основного критерия:
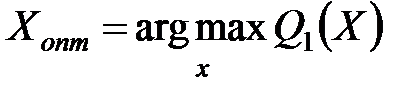 при условии, что
при условии, что 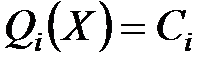 ,
, 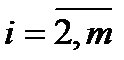
3. Введение суперкритерия. Данный метод предполагает свертку критериев, т.е. введение скалярной функции векторного аргумента:
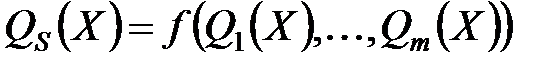
При определении вида функции f(Q(X)) можно использовать аксиоматический подход. Однако в большинстве случаев принятие аксиомы на практике разрушается. Лучше использовать прямое задание функции f(Q(X)).
Наиболее часто используют следующие виды функции:
1. Максиминная свертка основана на принципе эгалитаризма и ведет к увеличению уровня минимального или наихудшего критерия. Принцип эгалитаризма состоит в следующем: если у субъектов существуют оценки полезности, тот этот принцип максимизирует полезность наиболее слабого субъекта. Если нет ограничений, в частном случае, тот этот принцип приводит к равенству полезностей:
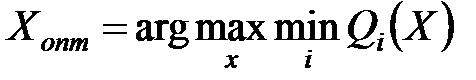
При этом предполагается, что Qi(x) пронормированны.
2. Аддитивная свертка основана на принципе утилитаризма и ведет к увеличению суммарной полезности, соответствует принципу абсолютной уступки, может допускать резкую дифференциацию критериев. Так называемое высокое значение суперкритерия может быть получено за счет высокого уровня одних локальных критериев при низких уровнях других критериев.
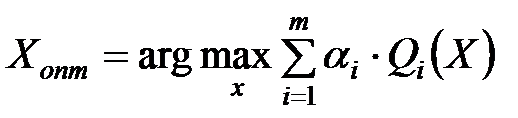 , где
, где 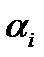 - вес i – ого критерия.
- вес i – ого критерия.
Похожий результат дает метод анализа иерархий в случае трехуровневой иерархии, где цель разбивается на критерии.
| Цель |
| Q1(X) |
| Qm(X) |
| X1 |
| Xn |
| … |
| … |
Это граф со слабыми связями, 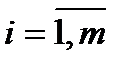 ,
, 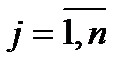 , qi – критерии, xj – альтернативные варианты.
, qi – критерии, xj – альтернативные варианты.
Метод анализа иерархий предполагает последовательную оценку влияния элементов нижнего уровня на элементы верхнего уровня. В результате получается оценка влияния каждого элемента самого нижнего уровня на общую цель. Соответственно выбирается та альтернатива в качестве наилучшей, влияние которой на общую цель максимально.
Влияние элементов нижнего уровня на верхний оценивается при помощи матрицы сравнения А: aij = 1/aji, что показывает уровень преобладания влияния элемента i над элементом j на элемент высшего уровня. Для оценки aij используется шкала отношений с нечетными цифрами от 1 до 9, где 1 – одинаковая значимость, одинаковое влияние, 9 – максимальное различие. При обработке матрицы А получается вектор приоритетов альтернатив, представляющий собой собственный вектор W матрицы A, что определяется по рекуррентному соотношению:
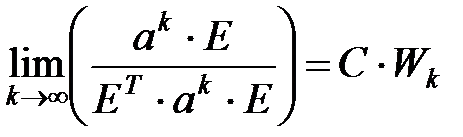
где Е – единичный вектор; k – номер итерации; С – константа.
Процесс продолжается до выполнения условия:
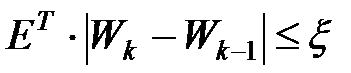 , где
, где 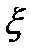 – зафиксированная погрешность.
– зафиксированная погрешность.
При k=1 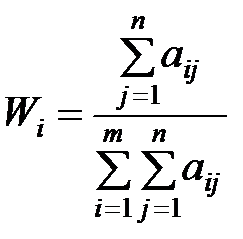 .
.
Для альтернатив x компоненты векторов-приоритетов в нашем случае будут являться пронормированными значениями критерия Qi(x). Аналогично определяются веса критериев. Составляется матрица парных сравнений для критериев. Компоненты векторов-приоритетов будут являться весами критерия 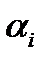 . Результирующий вектор приоритетов относительно цели определяется следующим образом:
. Результирующий вектор приоритетов относительно цели определяется следующим образом:
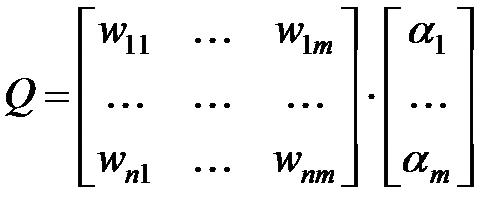
Первая матрица получается следующим образом: друг за другом записываются вектора приоритетов для каждого критерия.
При парном сравнении Qi(x) должно быть предварительно проранжированны:
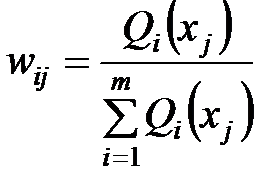 .
.
Обобщенная формула нахождения степени влияния любого j -го элемента n -го уровня на общую цель выглядит:
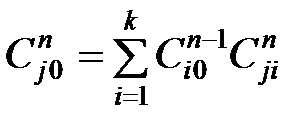
где k – число элементов в n-1 уровне; Ci0 – степени влияния элементов n-1 уровня на общую цель; Cji – степени влияния j -го элемента n -го уровня на элементы n-1 уровня.
В результате полученный при трехуровневой иерархии критерий аналогичен аддитивной свертке. Метод иерархий при трехуровневой свертке имеет достоинство: удобство оценивания альтернатив (для оценивания может использоваться как попарное сравнение, так и критерий). Кроме того, предполагается при анализе иерархий автоматическое нормирование и использование при необходимости большего числа уровней для анализа иерархий.
3. Мультипликативная свертка основана на принципе относительной уступки, которая снижает цену уступки для локальных критериев с большей величиной. Этот принцип близок принципу эгалитаризма. Этот вид свертки – что-то среднее между максиминной сверткой и аддитивной, но все же ближе к максиминной:
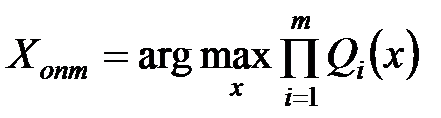
Все методы прямого оценивания предполагают нормирование критерия. Используются следующие способы нормирования:
1) Вводится понятие идеального качества операции Qi норм(X): 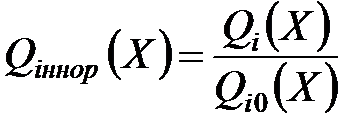 . В качестве идеального вектора выбираются заданные величины критериев, которые задаем сами.
. В качестве идеального вектора выбираются заданные величины критериев, которые задаем сами.
2) В качестве идеального вектора выбирается вектор, компонентами которого являются максимально возможные величины критериев Qi(X).
3) В качестве идеального вектора берется максимально возможный разброс вектора, т.е. разница между максимальным и минимальным значениями.
4) Расчет компонентов вектора приоритетов.
4. Поиск альтернативы с заданными свойствами. Этот метод используется в том случае, если заранее могут быть заданы значения локальных критериев 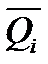 , называемые уравнениями притязания. Задача в этом случае сводится к приближению к идеальной точке
, называемые уравнениями притязания. Задача в этом случае сводится к приближению к идеальной точке 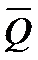 в m-мерном пространстве с использованием числовой меры близости.
в m-мерном пространстве с использованием числовой меры близости.
Например: 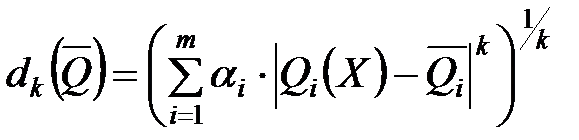
Дата публикования: 2014-10-19; Прочитано: 2463 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
