Модели развития и размещения производства

В качестве критерия выбираются минимальные затраты по производству и транспортировке. Это записывается в виде целевой функции. В качестве ограничений выступают ограничения по различным ресурсам.

Затем задача решается методом математического программирования.

Также в качестве критерия можно выбрать максимум загрузки мощностей. Однако с такой постановкой задачи модель становится очень сложной, что затрудняет ее решение и анализ. Поэтому иногда целесообразно разбивать модель на ряд этапов.

Рассмотрим пример, который связан с размещением и развитием производства электронной продукции на предприятиях корпорации. Особенность электронного продукта заключается в том, что затраты на перевозку значительно меньше затрат на производство. Соответственно вначале целесообразно не учитывать затраты на перевозку.

Объект – корпорация, состоящая из множества предприятий. Наша задача – спланировать производство однородной продукции, выпускаемой на предприятиях корпорации.

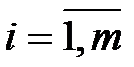– предприятия корпорации;

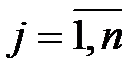– виды комплектующих или стадии производства;

m_i,j – производственные мощности i- того предприятия по j -тому процессу;

с_ij – себестоимость j -того комплектующего на i- том предприятии;

m_i,j+1 – максимальное количество комплектующих, которое может быть получено со стороны;

x_ij – количество комплектующих j -того вида, которые производятся на i- том предприятии;

q – количество готовых изделий, которое не должно превышать q_max – максимально определенного маркетинговыми исследованиями.

На первом шаге необходимо определить максимально возможный выпуск. Надо найти узкое место: 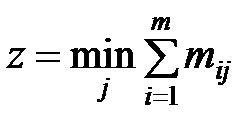с учетом внешних поставщиков, т.е. надо учесть m_i,j+1. Если найденное 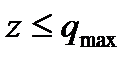(спрос), то оно не меняется, если же превышает, то меняется на q_max.

На втором шаге определяется задача размещения, т.е. на каком предприятии сколько комплектующих выпускать. Эту задачу надо решать для каждого вида комплектующих. В узком месте все производственные мощности должны быть загружены. Как быть с другими комплектующими, отличных от узких мест?

В качестве критерия выбираются затраты на производство, которые должны быть минимизированы:

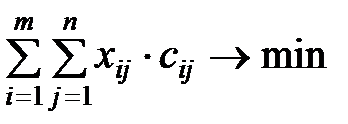
Ограничения: , .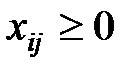

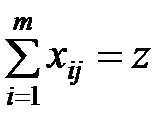На третьем шаге необходимо решить задачу развития производства. Предположим, что у корпорации есть финансовые средства, которые можно вложить в производство. Задачу имеет смысл решать, т.е. дальше развивать корпорацию, если рынок не насыщен.

Возникает вопрос: куда в первую очередь вкладывать средства, т.е. определить, на каком предприятии, в какое комплектующее вкладывать и размер вложений. Ответить можно следующим образом:

1. надо вкладывать в "узкое место" (т.е. определить номер комплектующего),

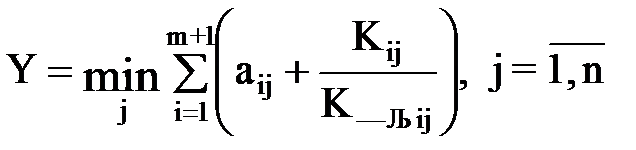
где Y – прирост объема производства; a_ij = M_ij – X_ij – "узкое место"; K_ij – капитальные вложения; K_удij – значения удельных капитальных вложений, необходимых для прироста мощностей на единицу. Прирост объема производства (Y) должен обеспечивать минимальные затраты.

2. в качестве критерия для определения номера предприятия нужно учитывать условие максимизации фондоотдачи, т.е. меньшие удельные капитальные вложения:

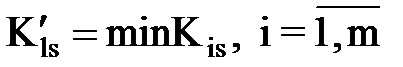, где

Здесь обозначим индекс мощностей S, которые первоначально оказались полностью загружены. Объем капитальных вложений должен быть таким, чтобы прирост мощностей по S -му элементу стал соответствовать “узкому месту” по прочим элементам.

3. чтобы определить размер вложений, надо свободные производственные мощности предприятия (не загруженные при выпуске конечной продукции в количестве Z шт.) 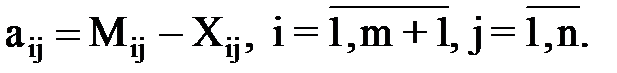умножить на величину кап. вложений:

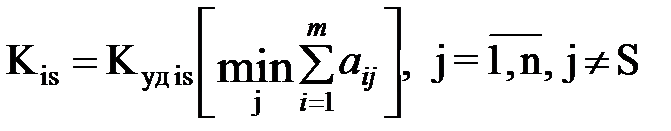
И так далее до тех пор, пока:

· не загрузим мощности по всем комплектующим одинаково;

· не насытим рынок;

· не кончатся деньги.

Теперь надо решить транспортную задачу, т.е. минимизировать транспортные издержки.

Есть поставщики и покупатели однородной продукции. Нужно определить, кто поставщик, а кто – потребитель. Если разница между комплектующими и сборкой больше нуля, то данное предприятие – поставщик, если меньше нуля – то потребитель. Затраты же от внешних поставщиков равны нулю. Далее решается транспортная задача.

Планирование и оптимизация работы предприятия.

Рассмотрим задачу оптимизации производственной программы. Предполагается, что предприятие выпускает различные виды изделий: .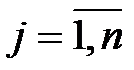

Производственная программа представляет собой годовой план выпуска.

x_ij – количество изделий j- того вида, которое является неизвестным.

Критерием работы предприятия является максимизация прибыли (также может быть минимизация затрат, максимизация выручки, выпуска продукции).

Ограничения по факторам производства (Т, З, К). Ограничение по капиталу должно быть обязательно. Ограничения относительно оборудования удобно рассматривать по фонду времени работы оборудования. По каждой группе оборудования считается свой фонд времени. Это главное ограничение, которое всегда присутствует в оптимизации производственной программы.

Ограничение по выпуску определяется при помощи маркетинговых исследований – ограничение по рынку сбыта и точке безубыточности.

Целевая функция может иметь вид:

§ Максимум прибыли, получаемой от реализации продукции:

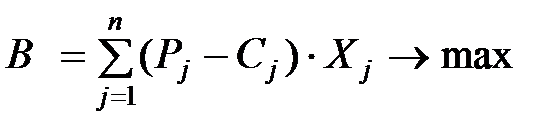
где P_j – цена j -го изделия,

С_j – себестоимость j -го изделия,

X_j – выпуск j-го изделия (в шт.)

§ Минимум себестоимости товарного выпуска:

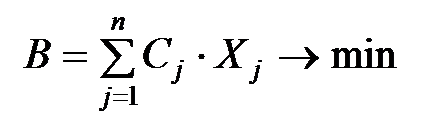
§ Максимум объема реализованной продукции:

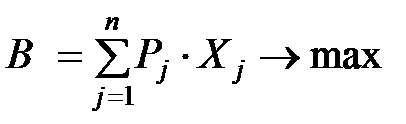
§ Если затраты разделить на переменные и постоянные, то функция прибыли примет вид:

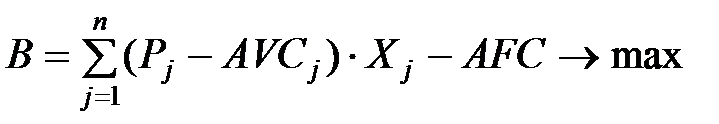
где AVC_j – переменные издержки производства j -го изделия,

AFC – постоянные издержки производства.

С точки зрения линейной модели последняя запись прибыли более корректна.

Ограничения:

§ по точке безубыточности имеют вид:

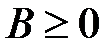, т.е.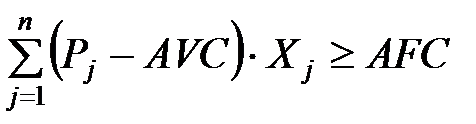

§ по рынку сбыта: 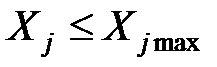. Два ограничения по точке безубыточности и по рынку сбыта составляют ограничение по выпуску.

§ по фонду времени работы оборудования:

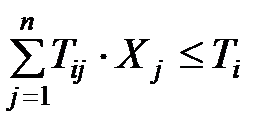
Где T_ij – трудоемкость;

T_i – фонд времени работы i – той группы оборудования;

§ по материалам: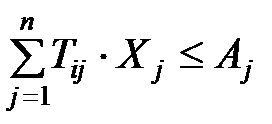

где T_ij – норма расхода i -го материала на производство единицы j -го изделия,

A_i – максимальный запас i -го материала.

Задача решается симплекс-методом. Для этого необходимо привести уравнение к каноническому виду, т.е. ограничения из неравенств следует привести к равенствам, вводя в левую часть дополнительную переменную x_n+1, т.е. при ограничениях типа

, , ,

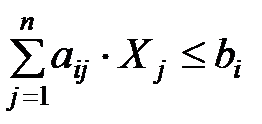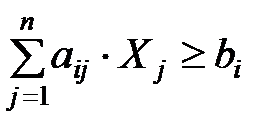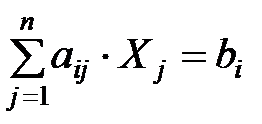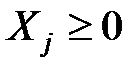
получаем:

a_i1 * x₁ + a_i2 * x₂ +…+ a_in * x_n + x_n+1 = b_i

a_i1 * x₁ + a_i2 * x₂ +…+ a_in * x_n – x_n+1 = b_i

Но для решения задачи на ЭВМ необходимо, чтобы новая переменная имела при себе коэффициент "+1", поэтому все второе выражение умножаем на "-1" и получаем:

- a_i1 * x₁ - a_i2 * x₂ -…- a_in * x_n + x_n+1 = - b_i

С каждой задачей линейного программирования связана другая линей­ная задача, называемая двойственной. Связь исходной и двойственной за­дачи в том, что решение одной из них может быть получено из решения другой. Решение двойственной задачи позволяет более глубоко проанали­зировать результаты.

Пусть предприятие выпускает 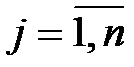видов продукции. Цена – P_j (в руб), выпуск – X_j (шт), расход i -го материала на производство j -го из­делия – a_ij. Тогда модель исходной задачи на максимум товарной продук­ции будет иметь вид:

,

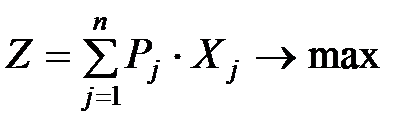
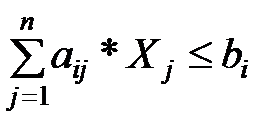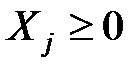
Для этого же предприятия можно сформулировать и двойственную за­дачу. Требуется найти такие оценки ресурсов Y_j (руб/кг), которые обес­печивали бы минимум общего расхода ресурсов в стоимостном выражении, а затраты на производство каждого вида продукции не были бы меньше его цены, т.е.

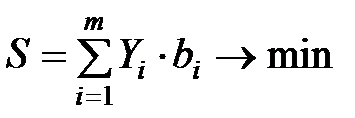
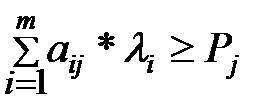
Прямая задача является задачей на max, а двойственная - на min. параметры целевой функции исходной задачи являются ограничениями двойственной задачи. Ограничения исходной задачи являются параметрами целевой функции двойственной задачи. Матрица коэффициентов a_ij исход­ной задачи транспонируется в двойственной задаче. Переменные Y_i назы­ваются оценками или учетными, неявными ценами ресурсов.

С математической точки зрения, двойственная оценка показывает, на сколько изменится целевая функция при изменении соответствующих ограничений на малую единицу.

Свойства двойственных оценок:

Свойство 1. 1) Если 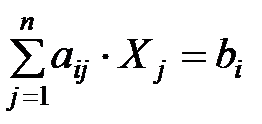, то X_n+1 = 0 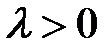, где X_n+1 – количество неизрасходованного ресурса, то данное выражение имеет следующий экономический смысл. Если ресурс расходуется полностью (равенство в ограничении), то он является дефицитным и его двойственная оценка, т.е. цена, больше нуля. Чем более дефицитен ресурс, тем больше двойственная оценка.

2) Если 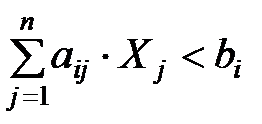, то X_n+1 > 0, 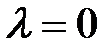. Экономический смысл: если ресурс расходуется не полностью, то его двойственная (или неявная) оценка равна нулю.

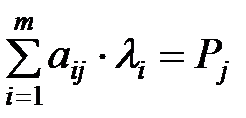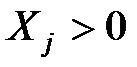Свойство 2. 1) Если , то . Экономический смысл: если издержки равны цене, то данная продукция выпускается, она выгодна (издержки измеряются в неявных ценах).

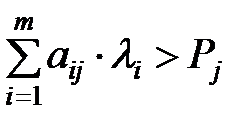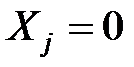2) Если, то . Экономический смысл: поскольку издержки больше цены, то изделие не выпускается.

Свойство 3. Для оптимального плана 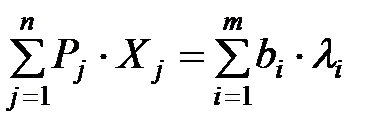, т.е. затраты на ресурсы равны стоимости товарной продукции. Для неоптимального плана: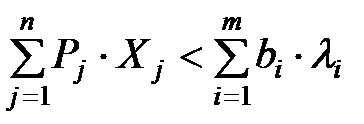

При решении задачи для определения производственной программы нужно выявить выгодную и невыгодную продукцию, чтобы сделать ее выгодной. Также нужно выявить узкое место, используя свойство 1.

Если рассматривать случай, когда затраты на единицу продукции c_j зависят от выпуска, то получим нелинейные целевую функцию и ограничения, таким образом, имеем задачу нелинейного программирования. Для решения следует применять метод множителей Лагранжа. Но практическую значимость имеет линейное программирование (оно снижает нелинейность). Округлять следует при решении в меньшую сторону, т.к. имеются ограничения на ресурсы.