Студопедия.Орг Главная | Случайная страница | Контакты | Мы поможем в написании вашей работы!  
 

Рішення в умовах конфлікту завжди пов’язані з ризиком!

⇐ Предыдущая6789101112131415Следующая ⇒


Для вибору відповідного господарського рішення в конфліктній ситуації використовують теорію ігор.

Мета теорії ігор – формування рекомендацій щодо оптимальної поведінки учасників конфлікту, тобто визначення оптимальної стратегії кожному з них.

       
   
 
 


Гра – математична модель конфлікту;

· гра з нульовою сумою (сума виграшів усіх гравців дорівнює нулю, тобто кожен виграє за рахунок інших);

· парна гра (грають два гравці);

· антагоністична гра (парна гра з нульовою сумою);

· матрична гра (скінченна парна гра з нульовою сумою).


Гравці – сторони у конфлікті;


· Виграш

· Програш результат гри;

· Нічия

Правила гри – перелік прав і обов’язків гравців;

Хід – вибір гравцем однієї з передбачених правилами

гри дій.

Ходи (1) особисті (свідомий вибір гравця);

випадкові (вибір дії, що не залежить від

волі гравця).

Ходи (2) скінченні (передбачають, скінчену

кількість ходів);

нескінченні (передбачають нескінчену

кількість ходів).

Стратегія гравця – сукупність правил, що визначають вибір варіанту дій у кожному особистому ході.

Оптимальна стратегія гравця забезпечує йому максимальний виграш.

Основне припущення для знаходження оптимального рішення в теорії ігор: супротивник такий же розумний, як і сам гравець!!!


У грі грають два гравці: А і В. (Себе прийнято ототожнювати з гравцем А). Нехай в А є m можливих стратегій: А1, А2,…А m, а в супротивника В – n можливих стратегій: В1, В2,…В n. Така гра називається грою m*n. Позначимо через аij виграш гравця А за власної стратегії А1 і стратегії супротивника Вj.

Зрозуміло, що можлива кількість таких ситуацій – m*n.

Гра може мати форму нормальну (матричну),

розгорнуту (у вигляді дерева).

Гру зручно відображати таблицею, що називається платіжною матрицею або матрицею виграшів. Вона має стільки стовпців, скільки стратегій у гравця В, і стільки рядків, скільки стратегій у гравця А. На перетині рядків і стовбців, що відповідають різним стратегіям, стоять виграші гравця А і, відповідно, програші гравця В.

З вигляду платіжної матриці можна встановити свідомо невигідні стратегії, для яких кожен з елементів відповідного рядка матриці менший або дорівнює відповідним елементом іншого будь–якого рядка (оскільки кожен елемент матриці – це виграш гравця А, і якщо для якої–небудь стратегії (рядка) всі виграші менші від виграшів іншої стратегії, зрозуміло, що перша стратегія менш вигідна аніж друга). Така операція відбраковування явно невигідних стратегій називається мажоруванням.

Для пошуку оптимальної стратегії вводять поняття верхньої та нижньої ціни гри.

Нижня ціна гри – елемент матриці, для якого виконується умова:

α=max min αij. (11.1)

i j

Вона показує, що хоча б яку стратегію застосував гравець В, гравець А гарантує собі виграш, не менший α.

Верхня ціна гри – елемент, що задовольняє умову:

β=min max αij. (11.2)

j i

Вона гарантує для гравця В, що гравець А не отримає виграш, більший за β.

Елемент матриці, для якого виконується умова

α=β, (11.3)

називається сідловою точкою.

У цій точці найбільший з мінімальних виграшів гравця А точно дорівнює найбільшому з максимальних програшів гравця В, тобто мінімум у якому-небудь рядку матриці збігається з максимумом у будь–якому стовбці.

Сідлова точка є розв’язком матричної гри, в якій міні-максним стратегіям притаманна стійкість.


При аналізі платіжної матриці можливі два варіанти оцінювання вибору:

І – платіжна матриця має сідлову точку;

ІІ – платіжна матриця не має сідлової точки.

І. За умови максимальної розумності гравців саме ці рядок та стовпець і являють собою оптимальні стратегії гравців. При використанні одним із гравців оптимальної стратегії іншому гравцеві невигідно відступати від своєї оптимальної стратегії, тобто стратегії, що відповідають сідловій точці, є найбільш вигідними для обох гравців.

Метод вибору стратегії на основі сідлової точки називається «принципом міні-макса», який інтерпретується: «чини так, щоб за найгіршої для тебе поведінки супротивника отримати максимальний виграш»

ІІ. Більш поширений варіант, коли користуються так званими мішаними стратегіями, тобто тими стратегіями, в яких випадковим чином чергуються особисті стратегії.

Оскільки кожен із гравців не знає, як поведе себе противник у даній ситуації, це вимагає застосування мінливої, гнучкої тактики.

Мішана стратегія гравця – це застосування всіх його чистих стратегій при багаторазовому повторенні гри в тих самих умовах із заданими ймовірностями.

Умови застосування мішаних стратегій:

· гра без сідлової точки;

· гравці використовують випадкове поєднання чистих стратегій із заданими ймовірностями;

· гра багаторазово повторюється в подібних умовах;

· під час кожного з ходів жоден з гравців не інформований про вибір стратегії іншим гравцем;

· допускається осереднення результатів ігор.

Коли гравець приймає рішення, керуючись чистою стратегією, то з усіх своїх варіантів він обере один, який і використає.

Якщо ж він діє відповідно до цієї стратегії, то розраховує (або апріорно задає) ймовірності кожного з можливих рішень.

Гравець А розраховує ймовірності р1, р2,…рm (причому, р1+р2+…+рm=1) застосування стратегій А1, А2,…,Аm, а гравець В – ймовірності g1,g2,…,gn застосування стратегій В1, В2,…,Вn, де g1+g2+…+gn=1.

Чисті стратегії гравця є єдино можливими неспільними подіями. Знаючи платіжну матрицю, можна визначити за заданих векторів р і g середній виграш (математичне сподівання) гравця А:

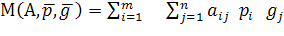, (11.4)

де р і g – вектори відповідних ймовірностей;

рі і gі – компоненти цих векторів.

Через застосування своїх мішаних стратегій гравець А намагається максимально збільшити свій середній виграш, а гравець А – довести цей ефект до мінімально можливого значення.

Гравець А прагне досягти виконання умови:

β=min max M 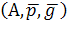. (11.5)

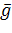
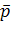
Гравець В домагається виконання іншої умови:

α= max min M 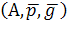. (11.6)

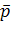
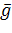
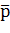Якщо 0 і 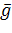0 – вектори, що відповідають оптимальним мішаним стратегіям гравців А і В, то:

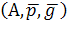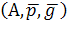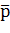min max M = max min M =М(А, 0, 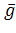0). (11.7)

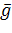
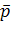
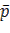
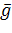
Ціна гри γ – середній виграш гравця А за умови виконання обома гравцями мішаних стратегій.

Розв’язок матричної гри:

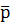· 0 – оптимальна мішана стратегія гравця А:

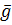· 0 – оптимальна мішана стратегія гравця В:

· γ – ціна гри.

Мішані стратегії будуть оптимальними (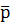 0 і 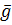0), якщо вони утворюють сідлову точку для функції М(А, 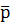0, 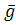0), тобто:

М(А, 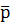0, 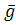0) ≥ M .

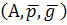За вибору оптимальних стратегій гравцю А завжди буде гарантований середній виграш, не менший, ніж ціна гри, за будь–якої фіксованої стратегії гравця В (а для гравця В - навпаки).

Активними стратегіями гравців А і В називають стратегії, що входять до складу оптимальних мішаних стратегій відповідних гравців з ймовірностями, котрі відмінні від нуля.

Суб’єкт господарювання за допомогою теорії ігор має можливість передбачити дії (ходи) своїх партнерів і конкурентів, але через складність її доречно використовувати тільки для прийняття одиничних, принципово важливих господарських рішень.

Приклад 1.

Спростити платіжну матрицю (табл.1) за рахунок відрахування явно невигідних стратегій.

Таблиця 1

Платіжна матриця

Стратегія гравців В1 В2 В3 В4
А1        
А2        
А3        
А4        
А5        
А6        

Розв’язання

У матриці всі елементи стратегії А3 менше за відповідні елементи

стратегії А1. Отже, стратегія А3 є невигідною порівняно зі стратегією А1 і може бути відкинута. Так само елементи стратегії А5 менші за відповідні елементи стратегії А2. Тому і стратегія А5 може бути відкинута (табл. 2).

Таблиця 2

Перетворена платіжна матриця

Стратегія гравців В1 В2 В3 В4
А1        
А2        
А4        
А6        

Приклад 2.

Знайти сідлову точку в грі, що характеризується платіжною матрицею (табл. 3).

Таблиця 3

Платіжна матриця

Стратегії гравців В1 В2 В3 В4 В5
А1 -50       -50
А2     -50 -60 -20
А3          
А4   -30   -10 -60

Розв’язання

α= max (-50; -60; 30; -60) =30;

β= (70; 30; 40; 60; 40)=30;

Висновок: точка на перетині стратегій А3 і В2 є сідловою.

Приклад 3.

Підприємства А та В конкурують на ринку збуту продукції. Кожне з них виробляє два види товарів:

А – товари виду а1 і а2;

В – товари виду b1 і b2.

Товари а1 і а2 та товари b1 і b2 мають приблизно однакові властивості. Ціна за одиницю товару а1 і b1 становить 10 грн., а2 – 20 грн., b2 - 5 грн. Ринок насичений цими товарами та розподілений так:

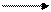а1: b1 1:1;

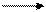а2: b2 1: 4.

Щодня на ринку продається по 2000 одиниць товару а1 і b1, 1000 одиниць а2, 4000 одиниць b2. Від продажу кожної одиниці продукції а1 і b1 отримується прибуток 2 грн., а а2 і b2 – 4 грн. Підприємство А бажає посісти провідне місце на ринку. Для цього у нього є такі можливості:

· знизити ціну на товар а1 до 9,5 грн. – у цьому випадку воно витисне з ринку товар b1 (А1);

· знизити ціну на товар а2 до 19 грн. – у цьому випадку, якщо ціна b2 не зміниться, то ринок на товари а2 і b2 розподілиться у співвідношенні 2:3 (А2).

Проаналізувавши ситуацію, підприємство А дійшло висновку, що підприємство В може відповісти так:

· нічого не робити у відповідь (В1);

· знизити ціну на товар b1 до 9,5 грн. (В2);

· збільшити обсяг продажу товару b2 на 25%, тоді В повністю витисне А з ринку товарів b2 (В3).

Передбачається, що у разі потреби кожне з підприємств може наситити ринок товарами.

Необхідно скласти платіжну матрицю для підприємства А.

Розв’язання

Можливості підприємств, що позначені відповідними літерами з індексами, являють собою їхні стратегії. Отже, платіжна матриця матиме розмір 2*3, оскільки в А є дві стратегії, а у В – три.

Елементи матриці обчислюються як виграш у новій ситуації порівняно зі старою, а саме:

елементи матриці = новий прибуток - старий прибуток

·

· а11: А знижує ціну на товар а1, а В не вживає жодних заходів. У цьому випадку А може продати не 2000, а 4000 одиниць товару а1:

а11=4000*1,5-2000*2=2000 (табл.)

· а12: А знижує ціну на товар а1, а В знижує ціну на товар b1 до 9,5 грн.:

а12=-2000*20+2000*1,5=-1000.

· а13:А знижує ціну на товар а1 і продає не 2000, а 4000 одиниць товару а1, але не продає жодної одиниці товару а2 тому, що весь ринок з а2 захоплює В:

а13=4000*1,5-200*2-1000*4=-2000.

· а21: А знижує ціну на товар а2 і В не вживає жодних заходів. Таким чином, А продає не 1000, а 2000 одиниць товару а2:

а21=2000*3-1000*4=2000.

· а22: А знижує ціну на товар а2, а В знижує ціну на товар b1, у цьому випадку А продає не 1000, а 2000 одиниць товару а2, але В повністю витісняє А з ринку товару а1:

а22=2000*3-1000*4-1000*2=0.

· а23: А знижує ціну на товар а2, а В збільшує випуск товарів b2 на 1000 одиниць і зовсім витісняє А з ринку товару а2:

а23=0-1000*4=-4000.

Таблиця 4

Платіжна матриця

Стратегії гравців В1 В2 В3
А1   -1000 -2000
А2     -4000

Висновок: аналіз матриці показує, що А виграє тільки в тому випадку, коли В не реалізує своїх стратегій. Отже, А не слід застосовувати жодної з аналізованих ним стратегій. Однак це не означає, що в А не має оптимальних стратегій. Просто їх не виявилося серед тих, що перевірялись.

⇐ Предыдущая6789101112131415Следующая ⇒


Дата публикования: 2015-09-18; Прочитано: 645 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

studopedia.org - Студопедия.Орг - 2014-2024 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.019 с)...