 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение и свойства двойного интеграла функции, заданной на прямоугольнике
|
|
Определение 1. Пусть 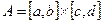 прямоугольник,
прямоугольник, 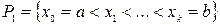 – разбиение отрезка
– разбиение отрезка 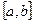 ,
, 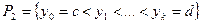 – разбиение отрезка
– разбиение отрезка 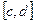 . Пару Р =(Р1, Р2) будем называть разбиением прямоугольника А.
. Пару Р =(Р1, Р2) будем называть разбиением прямоугольника А.
Определение 2. Прямоугольники  , на которые разбиение Р делит прямоугольник
, на которые разбиение Р делит прямоугольник 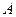 , мы будем называть прямоугольниками разбиения Р.
, мы будем называть прямоугольниками разбиения Р.
Определение 3.
 |
Пусть
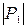 – диаметр разбиения Р1,
– диаметр разбиения Р1, 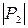 – диаметр разбиения Р2. Мы будем называть число
– диаметр разбиения Р2. Мы будем называть число 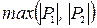 диаметром разбиения Р и обозначать
диаметром разбиения Р и обозначать 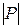 .
.
Различные параллелепипеды 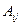 разбиения Р могут пересекаться лишь по своим границам. Площадь прямоугольника А равна сумме площадей прямоугольников разбиения Р.
разбиения Р могут пересекаться лишь по своим границам. Площадь прямоугольника А равна сумме площадей прямоугольников разбиения Р.
Определение 4. Пусть на прямоугольнике задана функция 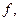
 – произвольная точка параллелепипеда
– произвольная точка параллелепипеда 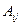 . Составим двойную сумму
. Составим двойную сумму
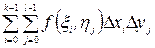 , (1)
, (1) 
котрую будем называть интегральной суммой.
Число I есть пределом интегральных сумм (1) при условии, что  , если
, если 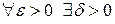 такое, что лишь только
такое, что лишь только 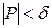 , неравенство
, неравенство
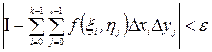
имеет место при любом выборе точек 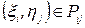 .
.
В том случае, когда предел I существует, его называют двойным интегралом и обозначают 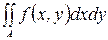 , а функцию f называют интегрируемой.
, а функцию f называют интегрируемой.
Двойной интеграл обладает теми же свойствами, что и интеграл Римана:
1. Если функция f непрерывна, то она интегрируема;
2. Пусть a и b – какие-либо числа, f и g – функции, интегрируемые на А. Тогда функция a f (х, у)+bg(х, у) интегрируема на А, и при этом
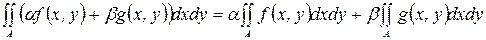 .
.
3. Если неотрицательная функция f интегрируема на А, то 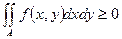 ;
;
4. Если f и g интегрируемые функции, и f (х, у)³g(х, у) "(х,y) ÎА, то 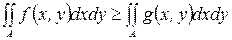 ;
;
5. Если f (х, у) интегрируема на А, то 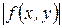 интегрируема на А, и при этом
интегрируема на А, и при этом
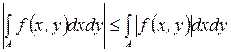 ;
;
6) Пусть f интегрируема на А, Р – произвольное разбиение А. Тогда f интегрируема на каждом  и
и
 .
.
Обратно, если найдется разбиение Р такое, что  и
и  существует
существует 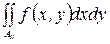 , то функция f интегрируема на прямоугольнике А.
, то функция f интегрируема на прямоугольнике А.
7) Если f (х, у)=С для "(х, у)ÎА, то
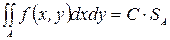 ,
,
где  – площадь прямоугольника А, которая равна
– площадь прямоугольника А, которая равна 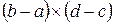 .
.
Дата публикования: 2015-09-17; Прочитано: 493 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
