 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Методах представления знаний
|
|
Заданы: дискретная область определения – аддитивный класс 2Х в пространстве Х на универсальном множестве Х; область значения – отрезок [0,1] на множестве действительных чисел.
Аксиома 4: функция множества А называется функцией принадлежности μ, если для любых 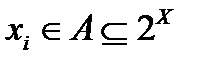 она отображает область определения на область значения:
она отображает область определения на область значения:
μ: 2X 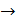 [0,1]. (1.10)
[0,1]. (1.10)
Каждому значению μ(xi) дается одна из следующих понятийных интерпретаций {1,2,3}:
1) нечеткость суждения 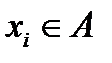 ;
;
2) субъективная совместимость xi и A;
3) мера нечеткости xi.
Обобщением данных свойств является понятие «нечеткость» (fuzzy) или принадлежность элемента xi множеству A.
Аксиома 5: нечеткое множество НМ есть совокупность упорядоченных пар- элементов множества А и соответствующих им значений функции принадлежности:
{|xi, μ(xi)|}, (1.11)
где А ={  {xi}}, i
{xi}}, i  I
I  {1,2,…n}.
{1,2,…n}.
Множество А называется носителем нечеткого множества.
На примере носителя А ={x1,x2,x3} и значений функций принадлежности μ(x1)=  , μ(x2)=μ2, μ(x3)=μ3 приведем основные формы записи нечётких множеств:
, μ(x2)=μ2, μ(x3)=μ3 приведем основные формы записи нечётких множеств:
А = {x1, x2, x3}, (1.12)
μA = μ1, μ2, μ3.
μ1/x1+μ2/x2+μ3/x3= 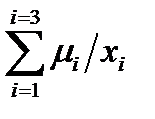 , (1.13)
, (1.13)
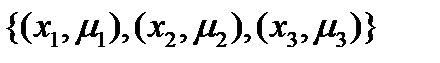 . (1.14)
. (1.14)
Каждое нечеткое множество может иметь многоуровневое представление в виде набора носителей, определенных для заданных значений μ:
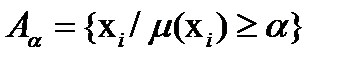 , (1.15)
, (1.15)
где Аα – носитель уровня α, т.е. подмножество на области определения, для элементов которого 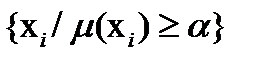 , i
, i  {1,2,..n}, /- связка «при».
{1,2,..n}, /- связка «при».
Например, если для нечетких множеств = {(x1, 0.2), (x2, 0.3), (x3, 0.5)} заданы уровни представления α=0,2 и α=0,3, то получим А0,2 = {x1,x2,x3} и A0,3 ={x2, x3}. Таким образом, данное нечеткое множество на уровнях 0,2 и 0,3 представлено 2-мя носителями: А0,2 = {x1,x2,x3} и A0,3 = {x2,x3}.
К любому нечеткому множеству, равному {(xi, μi)} с носителем А = {  {xi}} и
{xi}} и
i  I
I 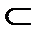 {1,2,…n}, можно добавить пару вида (xk, 0), k
{1,2,…n}, можно добавить пару вида (xk, 0), k 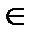 {1,2,…n} и k≠i.
{1,2,…n} и k≠i.
Такая процедура называется модификацией мощности носителя.
Базовые операции над нечеткими множествами с модифицированными носителями: нечеткое множество 1 есть {(xi, μi)} и нечеткое множество 2 равное
{(xi, 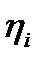 )}, i
)}, i  {1,2,…n}, сводятся к вычислению функции принадлежности результата {1,2,3,4}:
{1,2,…n}, сводятся к вычислению функции принадлежности результата {1,2,3,4}:
1) дополнение 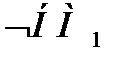 , γ=1-μi;
, γ=1-μi;
2) разность НМ1\НМ2, γ=MIN(μi,1- 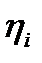 );
);
3) пересечение (произведение)  ∩
∩ 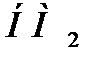 , γ= MIN (μi,
, γ= MIN (μi,  );
);
4) объединение (сумма) 

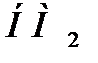 , γ=
, γ=  (μi,
(μi,  ).
).
1.7.Функции доверия и правило Демпстера А.Р., [23]
Заданы области: определения – аддитивный класс 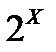 в пространстве
в пространстве 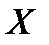 на универсальном множестве X; значения – отрезок [0;1] на множестве действительных чисел.
на универсальном множестве X; значения – отрезок [0;1] на множестве действительных чисел.
A. Ограниченность – Bel(ø)=0, Bel(X)=1;
B. Супераддитивность – для m множеств 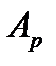
 X.
X.
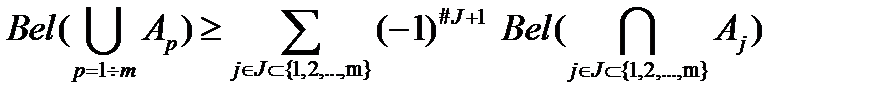 (1.16)
(1.16)
Понятийно Bel – это, по Г. Шеферу (G. Shafer) [24], мера доверия гипотезе, которой соответствует множество в аргументе функции.
Например, если имеется гипотеза: A есть одиночное множество {x1} или {x2}, или {x3}, то A={x1}  {x2}
{x2}  {x3} и мера доверия этой гипотезе будет равна Bel(A).
{x3} и мера доверия этой гипотезе будет равна Bel(A).
Рассмотрим частный случай: на множестве 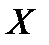 ={x1,x2} определены
={x1,x2} определены 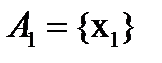 и
и  . Из супераддитивности функции доверия при m =2 следует:
. Из супераддитивности функции доверия при m =2 следует:
Bel({x1}  {x2})
{x2})  Bel({x1})+Bel({x2})-({x1}
Bel({x1})+Bel({x2})-({x1}  {x2}). (1.17)
{x2}). (1.17)
Из ограниченности функции доверия следует:
Bel({x1}  {x2})=Bel(ø)=0,
{x2})=Bel(ø)=0,
Bel({x1}  {x2})=Bel(
{x2})=Bel(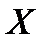 )=1. (1.18)
)=1. (1.18)
Используя формулу (1.17), в случае равенства и (1.18), получим:
Bel({x1})+Bel({x2})=1. (1.19)
Из (1.19), с учётом {x2}=  {x1}, вытекает:
{x1}, вытекает:
Bel( {x1})=1-Bel({x1}). (1.20)
{x1})=1-Bel({x1}). (1.20)
Соотношение (1.20) называется нормирокой Bel.
Рассмотрим применение нормированной функции доверия для обработки данных.
В 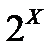 на x={x1,x2,…,xi,…,xn} определена Bel и результатом некоторого эксперимента или наблюдения в
на x={x1,x2,…,xi,…,xn} определена Bel и результатом некоторого эксперимента или наблюдения в 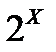 является факт, который известен в виде элемента xi и его значения функции принадлежности μi, то есть, как нечёткое множество НМ={(xi, μi)} с носителем {xi},
является факт, который известен в виде элемента xi и его значения функции принадлежности μi, то есть, как нечёткое множество НМ={(xi, μi)} с носителем {xi}, 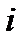 принадлежит {1,2,…,n}.
принадлежит {1,2,…,n}.
Аксиома 7. Функция доверия с простым носителем:
Bel={0, при A не включаемом в {xi};
μi при A, включенном в {xi}; 1- при A= 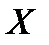 }, где
}, где  - множество из гипотез {1,2,3}:
- множество из гипотез {1,2,3}:
(1.21)
1) A есть любой элемент {xj}, кроме {xi};
2) A есть {xi}, или любой другой элемент {xj};
3) A есть универсальное множество X.
Рассмотрим теперь простейшую гипотезу: A есть однозначное множество {xi}. Дополнительно к свойствам нечёткого множества, эта гипотеза интерпретируется как определение меры доверия факту с помощью соотношения (1.21): Bel ({xi})=  .
.
Пусть теперь все экспериментальные данные сосредоточены на наборе, состоящем из двух фактов:
НМ={(xi, μi),(xj, μj)}с носителем {xi}  {xj},
{xj}, 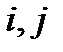 принадлежит{1,2,…,n}.
принадлежит{1,2,…,n}.
Аксиома 8:
Правило Демпстера: (композиция Bel({xi}) и Bel({xj})) при их объединении ({xi}  {xj}), не равна X:
{xj}), не равна X:
Bel({xi})  Bel({xj}) =
Bel({xj}) =  . (1.22)
. (1.22)
Выражение (1.22) определяет меру доверия двум фактам.
Если все экспериментальные данные сосредоточены на наборе, состоящем из m фактов НМ={(xi, 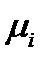 )} с носителем {
)} с носителем {  {xi}}, i
{xi}}, i  I
I 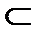 {1,2,…,n}, m=#I, то получаем композицию:
{1,2,…,n}, m=#I, то получаем композицию:
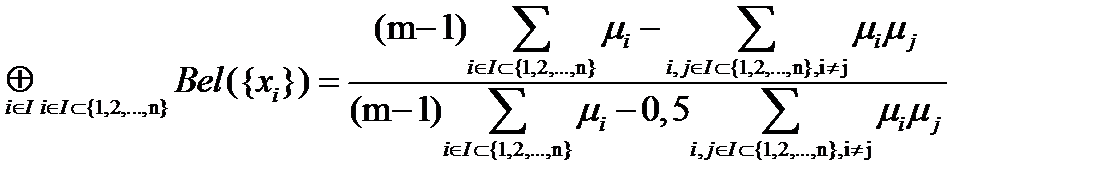 , (1.23)
, (1.23)
Выражение (1.23) определяет меру доверия набору из m фактов.
Дата публикования: 2015-09-17; Прочитано: 314 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
