Средняя квадратическая погрешность

функции вида Z =x₁ ± x₂ ± x₃ ±... ± x_n

Чтобы найти среднюю квадратическую погрешность функции данного вида, получим сначала среднюю квадратическую погрешность функции трех аргументов

Z = x₁ ± x₂ ± x₃.

Перепишем это равенство в следующем виде

Z = (x₁ ± x₂) ± x₃.

На основании формул (34) и (35) будем иметь

,

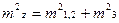где m_1,2 – средняя квадратическая погрешность функции (х₁+х₂).

Но 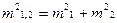. Тогда средняя квадратическая погрешность функции суммы или разности трех аргументов будет равна

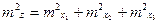
Рассуждая аналогичным образом для функций суммы или разности четырех, затем пяти и так далее аргументов, можно доказать, что для функций вида

Z = x₁ ± x₂ ± x₃ ±... ± x_n (36)

средняя квадратическая погрешность будет равна

,

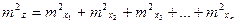или

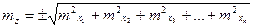, (37)

то есть средняя квадратическая погрешность функции суммы или разности многих независимых аргументов равна корню квадратному из суммы квадратов средних квадратических погрешностей аргументов.

Очевидно, что при равенстве средних квадратических погрешностей всех аргументов, формула (37) примет вид

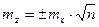, (38)

то есть средняя квадратическая погрешность функции суммы или разности многих n аргументов, измеренных с одинаковой точностью (средней квадратической погрешностью) в 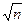раз больше средней квадратической погрешности одного аргумента.

Пример. В мостовой триангуляции все углы треугольников были измерены со средней квадратической погрешностью ± 5¢¢. Необходимо найти среднюю квадратическую погрешность суммы углов в треугольнике.

Для треугольника имеем функцию вида

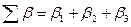
или согласно формулам (37) и (38)

.

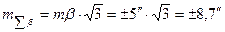Кстати говоря, из формулы (38) и данного примера можно сделать очень важный вывод: если задаться точностью (средней квадратической погрешностью) определения искомой величины, то можно заранее предвычислить точность последующих измерений. Например, с какой точностью необходимо измерять углы в треугольнике той же мостовой триангуляции, если задана предельная угловая невязка (для суммы углов). В этом случае формула (38) примет вид

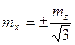. (39)

Для мостовой триангуляции, где возможно n число треугольников, формула (39) будет записана в следующем виде (формула Ферреро)

, (40)

где f_b - угловая невязка в треугольнике, n – число треугольников.