Системы линейных алгебраических уравнений

Определение. Системой линейных алгебраических уравнений (СЛАУ) называется система уравнений вида

Определение. Система называется однородной, если свободные члены равны нулю: Однородная система всегда является совместной - она имеет решение (возможно, не единственное).

Матрицы

называются матрицей системы и расширенной матрицей системы соответственно; столбцы

называются столбцом неизвестных и столбцом свободных членов соответственно. С учетом этих обозначений систему можно записать в матричной форме

Существует три основных метода решения совместной СЛАУ

а) правило Крамера;

б) матричный способ;

в) метод Гаусса.

а) Правило Крамера.

Обозначим

(определитель получается из D заменой i-го столбца на столбец свободных членов). Правило Крамера состоит в том, что при

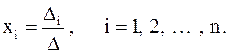
б) Матричный способ. Система совместна при и имеет единственное решение – столбец

в) Метод Гаусса. При решении методом Гаусса расширенную матрицу системы элементарными преобразованиями приводят к треугольному виду.

Пример. Решить систему

а) по правилу Крамера;

б) матричным способом;

в) методом Гаусса.

Решение. а) Имеем

Отсюда находим

б)

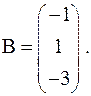
Найдем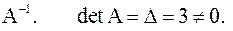

;

;

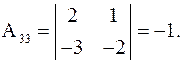
Поэтому .

Отсюда находим

.

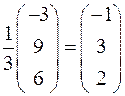Итак,

в) Решим систему методом Гаусса:

Ко второй строке прибавим первую, умноженную на три; из третьей строки вычтем вторую, умноженную на 2. Получим:

Третью строку умножим на 10, вторую на 7 и сложим их:

.

Последней матрице, имеющей треугольный вид (если исключить столбец свободных членов), соответствует следующая СЛАУ, равносильная исходной системе:

Из последнего уравнения находим , подставив его во второе уравнение, найдем и, наконец, подставив найденные и в первое уравнение, найдем :

Следует иметь в виду, что при решении СЛАУ методом Гаусса перестановка столбцов приводит к перенумерации неизвестных.