Метод прогонки розв’язування крайових задач для звичайних диференціальних рівнянь другого порядку

Нехай задане диференціальне рівняння:

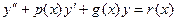(1)

(2)

де: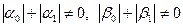

Де функції неперервна на

і розіб‘ємо точками:

Домовимось, що , ,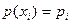

Замінивши похідні в (1) різницевими співвідношеннями, маємо:

(3)

(4)

Тоді: (5)

З крайових умов:

(6)

Розв‘яжемо (5) відносно змінної

(7)

Припустимо, що за допомогою повної системи рівнянь (5) вдалося з останнього рівняння виключити змінну , тоді з (7):

(8)

де: і - невідомі коефіцієнти.

Знайдемо формули для їх обчислення.

При з (7) маємо:

і з першого рівняння системи (6):

Після арифметичних перетворень маємо:

З другого боку з (8):

Таким чином отримаємо:

(9)

При з (8):

Підставивши знайдене значення в (7) маємо:

З (8) маємо:

(10)

З (9) і (10) можна послідовно обчислити і де - на цьому завершується прямий хід.

Підставивши в (8) замість , маємо:

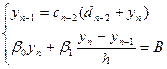
(11)

Використовуючи формули (8) і першу крайову умову з (6) ми можемо знайти

(12)