Доведення Теореми

Будемо вважати, що [а,в]=[0,1], бо можна це завжди досягнути шляхом заміни змінної.

Розглянемо многочлен Бернштейна:

(1)

Покажемо, що при великих n він задовольняє умови теореми.

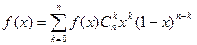(2)

Віднімемо від (1) - (2) матимемо:

(3)

Якщо f(x) неперервна на [0,1], то вона рівномірно неперервна, тобто:

"ε>0 $ : " є[0,1]:

ε

Візьмемо " х є[0,1]. Суму в (3) розіб‘ємо на дві:

де сумуємо по тих k для яких і

де сумуємо по тих k для яких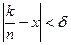

Позначимо через 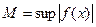, тоді оцінимо суму

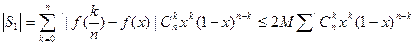
Згідно з Лемою2 при х є[0,1]:

, бо , ,

тоді якщо , то , тоді

Тоді:

Для :

Візьмемо такий, що , тоді

#

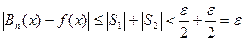
Зауваження: Справедливе твердження: Якщо f(x)є[0,1] має неперервну похідну до енного порядку включно, то: