Методи Рунге-Кутта

Задано диференціальне рівняння: (1) і початкова умова: .

Позначимо:

Вважатимемо, що має неперервні частинні похідні до деякого порядку 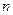, тоді розв‘язок має похідні порядку.

За формулою Тейлора:

Позначимо і відкинемо залишковий член:

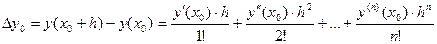(2)

Похідні які входять в праву частину (2) можуть бути обчислені:

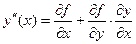
Похідні обчислюються досить складно, тому практично використовувати їх незручно.

Рунге запропонував:

(4)

Таку лінійну комбінацію з сталими коефіцієнтами

де:

де:

(4)

і - сталі коефіцієнти.

Причому .

(5)

Сталі вибираються так щоб розклади (2) і (4) по степенях співпадали до якомога більших степенів , тобто так, щоб функція:

(6)

так щоб (6) задовольняла умови:

але при цьому похибка:

Надаючи різні значення будемо отримувати різні формули Рунне-Кутта.

Необхідно наступні величини:

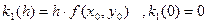
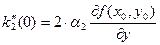
1. Нехай , тоді з (6):

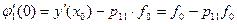
Тому:

В загальному випадку: , тобто (7)

2. , тоді

Таким чином отримаємо систему в якій кількість рівнянь менша ніж кількість невідомих:

(8)

Вибирати розв‘язки системи (8) треба так щоб отримувати якомога легші обчислення.