N. 3 середньоквадратичне наближення тригонометричними многочленами

Розглянемо простір функцій сумовних з квадратом на відрізку . Елемент найкращого наближення будемо шукати серед: - тригонометричний многочлен степеня 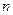. В якості лінійно-незалежної системи функцій беремо ортонормовану систему Розв’язавши систему (2) попереднього параграфа, отримаємо: , , 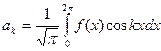. Тобто найкраще середньоквадратичне наближення для періодичної функції будуть давати частинні суми ряду Фур’є функції

§21

НАЙКРАЩЕ РІВНОМІРНЕ НАБЛИЖЕННЯ. ТЕОРЕМА ЧЕБИШЕВА

Якщо норма в лінійному просторі визначена не через скалярний добуток, то пошук елемента найкращого наближення ускладнюється.

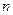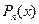Нехай - множина многочленів степеня не вище . Нехай також функція неперервна на і візьмемо . Відхилення функції від множини означається рівністю , нижню межу величини по всіх многочленах називають найменшим відхиленням.

Критерій за яким визначають елемент найкращого наближення дає теорема.

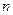Теорема Чебишева: нехай неперервна на . Для того щоб степеня не вище був многочлен найкращого рівномірного наближення для функції необхідно і достатньо щоб на відрізку існувала хоча б одна система з -х точок в якій різниця задовольняла б наступні умови:

• Почергово змінює знак
• Набуває найбільшого по модулю значення на .

Ці дві умови можна записати так:

Означення: система про яку їде мова в теоремі називається чебишевським альтернантом.

Означення: точка , або називатимемо е-точкою.

Означення: якщо в е-точці виконується , то точку називають “+” точкою, а якщо , то “-” точкою.