Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами

Нехай задане диференціальне рівняння:

(1)

і крайові умови: (2) або

(2‘)

(2 )

Потрібно знати розв‘язок диференціального рівняння у вигляді таблиці значень на .

Розіб‘ємо на частини точками:

, ,

Другу похідну в рівнянні (1) замінимо різницевим відношенням:

Тоді отримаємо систему:

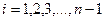(3)

В залежності від крайових умов до системи (3) будуть додані рівняння:

(4)

(4‘)

Враховуючи формули чисельного диференціювання функцій інтерполювання многочленами Ньютона.

або

(4‘‘)

Отримаємо систему рівнянь з невідомими. Дана система буде мати єдиний розв‘язок якщо відповідна однорідна система (випадок коли ) матиме лише тривіальний розв‘язок.

Введемо позначення:

Лема1. Нехай дана довільна система з точок:

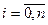Якщо , для довільного , то найбільшим додатнім числом серед може бути 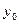або .

Нехай - найбільше додатне число, .

Тоді існують числа , . Маємо:

, тоді випливає

, тобто

, що неможливо.

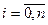Лема2. Якщо задана система точок і виконується умова , , то найменшим від‘ємним числом серед може бути лише 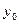або .

Доведення аналогічне.

Доведемо, що система (3) з крайовими умовами (4), (4‘), (4‘‘) має лише тривіальний розв‘язок у випадку коли .

1. Нехай маємо (3) і умови (4). Якщо існує ненульовий розв‘язок, то серед чисел є найбільше додатне або найменше від‘ємне, а це суперечить Лемі 1 або 2.

2. Нехай маємо (3) і умови (4‘), маємо:

Якщо існує ненульовий розв‘язок, то серед чисел є найбільше додатне або найменше від‘ємне. Знову суперечність з Лемою 1 або 2.

3. Система (3) і умови (4‘‘): і хоча б одне з них не дорівнює 0. Тоді в (3) підставимо :

Визначивши з () і підставимо в ( ).

(5)

Аналогічне підставивши в систему (3) маємо:

З останньої системи можна визначити:

(6)

Розглянемо рівності (5) і (6). Нехай знову існує деякий нетривіальний розв‘язок системи, тоді найбільше додатне або найменше від‘ємне число можуть бути 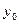або .

Нехай 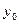- найбільше додатне число, тоді крок виберемо настільки малим щоб:

, тоді з (5):

, що неможливо з Лемою.

Щоб отримати таблицю розв‘язків диференціального рівняння при всіх розглянутих крайових умовах слід розв’язати одним з відомих способів систему (3) і (4) або (4‘) або (4‘‘).

Якщо позначити наближений а 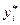- точний розв‘язки, тоді величина: 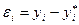вказує похибку в вузлі . Можна довести, що похибка оцінюється таким співвідношенням:

(7)

Заваження1: Розглянутий метод можна застосувати також для рівнянь виду:

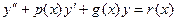(8)

з умовами:

(9)

Якщо другу похідну замінити так само як в попередніх випадках, а першу похідну так:

, отримаємо:

(10)

Зауваження2: Похідні замінюють таким співвідношенням:

(11)

В усіх розглянутих випадках похибка оцінюється нерівністю (7).