 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Означення: Різницевим рівнянням називається рівняння відносно функції дискретної змінної
|
|
Розглянемо найпростіший випадок одного лінійного рівняння відносно невідомої функції одного цілочисельного аргументу.
 (1)
(1)
Відмітимо, що це рівняння називається лінійним різницевим рівнянням к-того порядку. Воно є дискретним аналогом лінійного диференціального рівняння порядку k рівняння:  .
.
Означення: Рівняння  (2) називається лінійним однорідним різницевим рівнянням.
(2) називається лінійним однорідним різницевим рівнянням.
Теорема: Якщо  є деякий частинний розв’язок рівняння (1), то
є деякий частинний розв’язок рівняння (1), то  є розв’язком однорідного рівняння (2).
є розв’язком однорідного рівняння (2).
Означення: Система  розв’язок рівняння (2) називається лінійно незалежною, якщо з того, що
розв’язок рівняння (2) називається лінійно незалежною, якщо з того, що 
Теорема: Якщо деякі функції  є розв’язком однорідного рівняння (2), то лінійна комбінація
є розв’язком однорідного рівняння (2), то лінійна комбінація  теж є розв’язком рівняння (2)
теж є розв’язком рівняння (2)
Мають місце наступні твердження:
1. Загальний розв’язок неоднорідного рівняння дорівнює сумі його частинного розв’язку і загального розв’язку відповідного однорідного рівняння.
2. Якщо функції  є розв’язками однорідного рівняння (2), то
є розв’язками однорідного рівняння (2), то  теж є розв’ язком рівняння (2).
теж є розв’ язком рівняння (2).
3. Якщо  , то загальний розв’ язок рівняння (2) можна записати у вигляді:
, то загальний розв’ язок рівняння (2) можна записати у вигляді:  , де
, де  - лінійно-незалежні розв’ язки рівняння (2).
- лінійно-незалежні розв’ язки рівняння (2).
Означення: Якщо в рівняннях (1) і (2) коефіцієнти  не залежать від
не залежать від 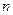 , то такі рівняння називаються рівняннями з сталими коефіцієнтами.
, то такі рівняння називаються рівняннями з сталими коефіцієнтами.
 (
( )
)
 (
( )
)
розв’ язок рівняння (2) будемо шукати у вигляді:  . Тобто
. Тобто  .
.
Бачимо, що кожному кореню рівняння  відповідає частинний розв’ язок рівняння (
відповідає частинний розв’ язок рівняння ( ), а саме
), а саме  . Якщо всі корені характеристичного рівняння прості, то маємо к-різних розв’язків. Якщо деякий корінь має кратність
. Якщо всі корені характеристичного рівняння прості, то маємо к-різних розв’язків. Якщо деякий корінь має кратність  , то йому відповідають розв’язки:
, то йому відповідають розв’язки:  ,
,  , …,
, …, 
 .
.
§17
МНОГОЧЛЕНИ ЧЕБИШЕВА.
 - позначаються,
- позначаються, 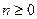 . Задаються наступними рівностями:
. Задаються наступними рівностями:  ,
,  ,
,  . (1) Використовуючи рекурентні формули (1), отримаємо:
. (1) Використовуючи рекурентні формули (1), отримаємо:  ,
, 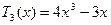 .
.
Відмітимо, що коефіцієнт біля  в многочлена
в многочлена  дорівнює
дорівнює  , всі многочлени з індексами
, всі многочлени з індексами  - парні, з індексами
- парні, з індексами  - непарні.
- непарні.
Відомо, що  ,
,



Позначимо  .
.
Отримаємо:  .(2)
.(2)
Порівнюючи (1) і (2) бачимо, що функція  задовольняє рекурентне співвідношення (1). Початкові умови:
задовольняє рекурентне співвідношення (1). Початкові умови:  ,
,  . Таким чином:
. Таким чином:
 (3). З даної рівності випливає, що
(3). З даної рівності випливає, що  при
при  . (4)
. (4)
Зауваження: нерівність (4) не буде справедливою при всіх  . Якщо
. Якщо 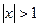 , то
, то  , а
, а 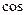 такого числа не завжди менше 1.
такого числа не завжди менше 1.
Рекурентне співвідношення (1) є різницевим рівнянням. Позначимо  , тоді отримаємо характеристичне рівняння:
, тоді отримаємо характеристичне рівняння: 


Якщо 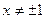 , то корені прості, а тому
, то корені прості, а тому  . Замість
. Замість 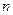 підставимо 1, отримаємо:
підставимо 1, отримаємо:  або
або 

 .
.
Тому  . (5) – многочлен Чебишева
. (5) – многочлен Чебишева
Зауваження: з нерівностей (4) випливає, що многочлени Чебишева набувають  значення тоді, коли
значення тоді, коли 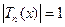 ,
,  ,
,  ,
,  , де
, де 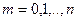 .
.
Означення: Многочлен  називають многочленом, який найменше відхиляється від нуля. Таке означення пояснюється наступною теоремою:
називають многочленом, який найменше відхиляється від нуля. Таке означення пояснюється наступною теоремою:
Теорема: Якщо  з старшим коефіцієнтом рівним одиниці, то
з старшим коефіцієнтом рівним одиниці, то  .
.
Теорема доводиться методом від супротивного.
Заміною змінної  проміжок
проміжок  переводимо взаємно однозначно в проміжок
переводимо взаємно однозначно в проміжок  . Тоді многочлен
. Тоді многочлен  з старшим коефіцієнтом
з старшим коефіцієнтом  називається многочленом Чебишева на
називається многочленом Чебишева на  . Аналогічно як ми робили для
. Аналогічно як ми робили для  , можна побудувати многочлен, який найменше відхиляється на
, можна побудувати многочлен, який найменше відхиляється на  .
.
Цей многочлен запишеться: 

Розглянемо значення многочленна 
Отримали, що многочлен  степеня n-1 має n нулів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.
степеня n-1 має n нулів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.
§18
Дата публикования: 2014-11-18; Прочитано: 535 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
