Определение. Каноническим базисом в пространстве трехмерных геометрических векторов называют векторы , которым соответствуют канонические векторы

Каноническим базисом в пространстве трехмерных геометрических векторов называют векторы , которым соответствуют канонические векторы 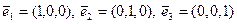ортонормированного базиса в трехмерном арифметическом пространстве. Аналогично определяется канонический базис 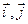в пространстве двумерных геометрических векторов.

Как следует из определения векторы образуют ортонормированный базис.

Определение. Числовой проекцией 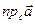вектора на вектор 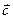называют число, найденное как скалярное произведение вектора на орт вектора 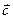, так что .

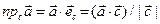Как следует из определения, числовые проекции вектора на векторы канонического базиса совпадают с компонентами 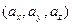вектора . Отметим, что если в реальном пространстве выбран базис, отличный от канонического, то координаты вектора в этом базисе отличаются от исходных компонент 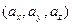вектора .