Теорема (неравенство Коши – Буняковского )

Для любых двух векторов и евклидова пространства справедливо неравенство , называемое неравенством Коши – Буняковского.

Доказательство. Если хотя бы один из двух векторов и нулевой, то доказываемое неравенство превращается в равенство и является справедливым.

Рассмотрим далее случай, когда оба вектора , отличны от нулевого вектора. В силу аксиомы Е4 справедливо неравенство для любого вещественного числа . На основании аксиом Е1 – Е3 это неравенство можно переписать в следующем виде . Полученное квадратное неравенство относительно параметра при положительном значении коэффициента выполняется тогда и только тогда, когда дискриминант соответствующего квадратного уравнения меньше или равен нулю. Таким образом, , откуда и следует доказательство справедливости неравенства Коши – Буняковского.

После того, как в линейном пространстве введено скалярное произведение, можно определить такие метрические понятия как длина вектора и угол между векторами.

Определение. Длина (модуль) любого вектора в евклидовом пространстве определяется как арифметическое значение корня из скалярного произведения и обозначается . Таким образом, .

Длина вектора равна нулю тогда и только тогда, когда вектор нулевой вектор.

Вектор 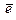, длина которого равна единице, называется нормированным, единичным или ортом. Переход от вектора к вектору называют нормированием вектора .

Определение. Компоненты любого нормированного вектора 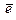в евклидовом пространстве называют направляющими косинусами.

Любой ненулевой вектор можно нормировать, умножив его на величину обратную его модулю. Действительно,

В евклидовом пространстве арифметических векторов 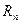длина любого вектора из этого пространства вычисляется по формуле .

Пример. Пусть задан трехмерный арифметический вектор Длина вектора вычисляется по определяющей формуле Орт вектора имеет вид . Соответственно, направляющие косинусы вектора равны Если вектор изображается в декартовой прямоугольной системе координат , то по направляющим косинусам можно найти и изобразить углы между вектором и осями .

Следствие (неравенство треугольника). Для любых векторов и евклидова пространства выполняется неравенство . Действительно,

.

Отсюда, , что и требовалось доказать.

В реальном пространстве это неравенство означает, что длина одной из сторон треугольника, меньше суммы длин двух других его сторон.

Определение. Углом между любыми ненулевыми векторами и евклидова пространства называется угол из диапазона , косинус которого определяется по формуле . Таким образом, .

При этом из неравенства Коши – Буняковского, представленного в виде , следует, что вычисляемое по формуле значение косинуса угла удовлетворяет необходимому для любого косинуса угла условию

Определение. Любые векторы и евклидова пространства называют ортогональными и обозначают как , если их скалярное произведение равно нулю.

Как следует из сформулированных определений, наименьший угол между ортогональными векторами в реальном пространстве равен девяносто градусов.

Следствие (теорема косинусов). Для любых ненулевых векторов и евклидова пространства выполняется равенство .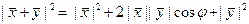

Действительно, .

Следствие (теорема Пифагора). Для любых ненулевых ортогональных векторов и евклидова пространства выполняется равенство .

В реальном пространстве это равенство означает, что квадрат длины гипотенузы треугольника, равен сумме квадратов длин катетов.

Определение. Система векторов евклидова пространства называется ортогональной, если скалярное произведение любой пары векторов системы равно нулю.