Векторное и смешанное векторно-скалярное произведения

Определение. Векторным произведением двух геометрических векторов 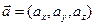и 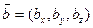в реальном пространстве называют геометрический вектор 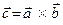, представление которого в каноническом базисе имеет вид

При решении практических задач, представление вектора 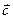в каноническом базисе находят, формально раскрывая по первой строке определитель третьего порядка .

Отметим, что векторное произведение, в отличие от скалярного произведения, определено только в реальном пространстве и только для геометрических векторов.

Непосредственно из определения следуют алгебраические свойства векторного произведения: ; ; .

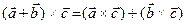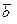Определение. Два любых вектора и линейного пространства называются коллинеарными, если они линейно зависимы.

Непосредственно из определений коллинеарности и линейной зависимости двух векторов следует, что нулевой вектор коллинеарен любому вектору. Если оба вектора и 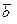отличны от нулевого, то один вектор может быть линейно выражен через другой по формуле , где 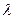- некоторое вещественное число.

Пример. Пусть и есть двумерные арифметические векторы. Они линейно зависимы, так как . Таким образом, векторы и 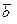являются коллинеарными. Кроме того, вектор 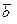может быть линейно выражен через вектор по формуле , так как .

Определение. Три любых вектора , , 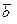линейного пространства называются компланарными (лежащими в одной плоскости), если они линейно зависимы.