 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема (основные свойства ортонормированного базиса)
|
|
1. Координаты произвольного вектора в ортонормированном базисе равны скалярным произведениям этого вектора на соответствующие векторы этого базиса.
2. Скалярное произведение двух любых векторов вычисляется в ортонормированном базисе как сумма произведений соответствующих координат в данном базисе.
Доказательство. Пусть  есть некоторое разложение произвольного вектора
есть некоторое разложение произвольного вектора  в ортонормированном базисе
в ортонормированном базисе 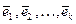 . Последовательно и скалярно умножая обе части этого равенства на векторы базиса, получим
. Последовательно и скалярно умножая обе части этого равенства на векторы базиса, получим
 для всех
для всех  ,
,
что и требовалось доказать в первой части теоремы.
Пусть далее  ,
,  есть некоторое разложение произвольных векторов
есть некоторое разложение произвольных векторов  в ортонормированном базисе
в ортонормированном базисе 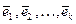 . Составим скалярное произведение векторов
. Составим скалярное произведение векторов  , и в силу аксиоматических свойств любых скалярных произведений и свойств ортонормированного базиса получим:
, и в силу аксиоматических свойств любых скалярных произведений и свойств ортонормированного базиса получим:
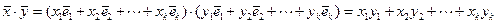 ,
,
что и требовалось доказать.
Определение. Два любых вектора 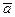 ,
,  линейного пространства имеют одинаковое (одно и то же) направление, если для них выполняется условие
линейного пространства имеют одинаковое (одно и то же) направление, если для них выполняется условие  .
.
Определение. Арифметические векторы 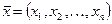 в задачах с геометрической терминологией называют точками
в задачах с геометрической терминологией называют точками  с компонентами
с компонентами  .
.
В частности, арифметические векторы  из
из 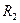 или
или  из
из  также называются точками и изображаются в декартовой прямоугольной системе координат в виде точек
также называются точками и изображаются в декартовой прямоугольной системе координат в виде точек  или
или  . При этом все координаты измеряются в одинаковом масштабе, причем первую координату называют абсциссой, вторую – ординатой, а третью – аппликатой. Точку
. При этом все координаты измеряются в одинаковом масштабе, причем первую координату называют абсциссой, вторую – ординатой, а третью – аппликатой. Точку  или
или  будем называть началом координат на плоскости или в пространстве.
будем называть началом координат на плоскости или в пространстве.
Дата публикования: 2014-11-18; Прочитано: 1699 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
