Евклидовы пространства

Определение. Скалярным произведением двух любых векторов линейного пространства называется правило, по которому каждой упорядоченной паре векторов из ставится в соответствие вещественное число. Скалярное произведение обычно обозначают Скалярное произведение должно удовлетворять следующим четырем аксиомам:

Е1.

Е2.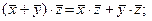

Е3.

Е4. причем тогда и только тогда, когда

Линейное пространство называется евклидовым пространством, если в нем введено скалярное произведение. В дальнейшем рассматриваются только вещественные евклидовы пространства, т.е. числа будут только вещественными.

Укажем простейшие следствия аксиом Е1 – Е4.

1.

2.

3.

4.

Рассмотрим вещественное арифметическое пространство 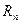. Для любых двух векторов этого пространства и 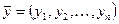определим их скалярное произведение по правилу: . Введенное таким образом правило удовлетворяет четырем аксиомам скалярного произведения, что непосредственно следует из соответствующих свойств вещественных чисел.