Базис конечномерного векторного пространства

V – конечномерное векторное пространство над полем P, S – система векторов (конечная или бесконечная).

Определение 8.10. Базисом системы S называется ее подсистема S ´ такая, что

• подсистема S ´ линейно независима;

• любой вектор системы S линейно выражается через векторы системы S ´.

Как и для арифметических n -мерных векторных пространств верна следующая теорема:

Теорема 8.5. Любые два базиса одной и той же системы векторов состоят из одинакового количества векторов.

Теорема 8.6. В конечномерном векторном пространстве любая система, содержащая хотя бы один ненулевой вектор, имеет базис.

Определение 8.11. Базисом конечномерного векторного пространства V называется система векторов этого пространства, такая что

• эта система линейно независима;

• каждый вектор из V линейно выражается через векторы базиса.

Теорема 8.7. В n -мерном векторном пространстве есть базис. При этом базисы – это в точности все системы, состоящие из n линейно независимых векторов, то есть

- базис – это система, состоящая n из линейно независимых векторов, и

- любая система, состоящая из n линейно независимых векторов, является базисом.

Определение 8.12. Размерностью пространства называется количество векторов в любом его базисе.

Пример 8.5. Приведем примеры базисов конечномерных векторных пространств.

1) Пространство V = Rⁿ. Система единичных векторов e ₁, e ₂, …, e_n образует базис этого пространства, что следует из свойств этой системы векторов. Размерность Rⁿ равна n.

2) Пространство V = R ³. Система векторов e ₁, e ₂, e ₃ – базис R ³. Любой другой базис этого пространства состоит из трех линейно независимых векторов, это, например, векторы а ₁, а ₂, а ₃: а ₁ = (2, 3, –1), а ₂ = (0, 4, 7), а ₃ = (0, 0, –4). Эти векторы образуют лестничную систему, поэтому они линейно независимы. Размерность R ³ равна 3.

3) Пространство V = R ^2´2. В качестве базиса этого пространства можно выбрать векторы Е ₁ = 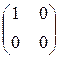, Е ₂ = 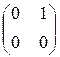, Е ₃ = 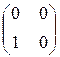, Е ₄ = 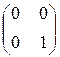. Можно показать, что они линейно независимы. Как выражаются элементы пространства через векторы базиса, видно из следующего примера: если вектор A = 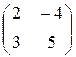, то А = 2 Е ₁ + (–4) Е ₂ + 3 Е ₃ + 5 Е ₄. Размерность R ^2´2 равна 4.

4) Пространство V = R [ x ]_(£3). Векторы f ₁ = 1, f ₂ = x, f ₃ = x ², f ₄ = x ³ образуют базис пространства R [ x ]_(£3). Линейная независимость этих векторов легко доказывается, произвольный вектор f = a + bx + cx ² + d x ³ выражается через векторы следующим способом f = a × f ₁ + b × f ₂ + c × f ₃ + d × f ₄. Размерность этого пространства равна 4.

5) Пространство направленных отрезков. На плоскости базис состоит из любых двух неколлинеарных векторов, в пространстве – из любых трех некомпланарных векторов.