Тригонометрическая форма комплексного числа

Вектор можно задать не только координатами в прямоугольной системе координат, но и длиной и углом, который он образует с некоторым фиксированным направлением (полярная система координат), т. е. задать вектор полярными координатами (рис. 1.11).

Определение 1.21. Длина вектора, соответствующего комплексному числу z (или расстояние от начала системы координат до точки, изображающей комплексное число) называется модулем комплексного числа и обозначается | z | = r.

Определение 1.22. Радианная мера угла, образованного этим вектором с положительным направлением действительной оси Ох называется аргументом комплексного числа z и обозначается Аrg z = j.

Другими словами, аргумент комплексного числа – это угол между положительной полуосью Ох и лучом Oz.

Число ноль изображается нуль-вектором, для него модуль равен 0, аргумент нуля не определен. Для ненулевого комплексного числа z аргумент определяется с точностью до 2p k, где k – любое целое число.

Главным значение аргумента называется такое значение j, что
j Î (–p, p]. Часто главное значение аргумента обозначается аrg z. Главное значение аргумента обратного комплексного числа отличается знаком аргумента исходного, т. е. аrg = – аrg (z).

Для комплексного числа z = a + bi установим связь между числами a, b и r, j, т. е. между декартовыми и полярными координатами.

Рассмотрим прямоугольный треугольник OMK (рис. 1.11), по теореме Пифагора имеем: OM ² = OK ² + MK ² Þ r ² = a ² + b ² Þ r = , a = r × cos j, b = r × sin j. Тогда z = a + b × i = r × cos j + r × sin j× i = r (cos j + i × sin j).

Определение 1.23. Выражение z = r (cos j + i × sin j) называется тригонометрической формой комплексного числа.

Формулы перехода от алгебраической формы комплексного числа z = a + b × i к тригонометрической следующие:

r = , sin 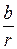j = = , cos j = = .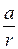

Если a ≠ 0, то tgj = . Можно найти аргумент числа z, пользуясь правилом:

a > 0 Þ j = ,

a < 0 Þ j = + p,

a = 0 Þ 1) b > 0 Þ j = , 2) b < 0 Þ j = – .

Определение 1.24. r ₁(cos j₁ + i × sin j₁) = r ₂(cos j₂ + i × sin j₂) Û r ₁ = r ₂ и j₁ = j₂ + 2p k, k Î Z.

Пример 1.12. Представить следующие комплексные числа в тригонометрической форме: z ₁ = – i, z ₂ = –3 i, z ₃ = –8,
z ₄ = –2(cos – i × sin ),

Решение. а) z ₁ = – i Þ a = , b = –1. Найдем модуль и аргумент данного числа: r = = = 2; т. к. a = > 0, то j = = = – .

Окончательно получаем тригонометрическую форму z ₁ = – i =
= r (cos j + i × sin j) = 2(cos + i × sin ).

б) z ₂ = –3 i Þ a = 0, b = –3. Найдем модуль и аргумент данного числа: r = = = 3; т. к. a = 0 и b < 0, то j = – .

Получаем z ₂ = –3 i = r (cos j + i × sin j) = 3(cos + i × sin ).

в) z ₃ = –8 Þ a = –8, b = 0. Найдем модуль и аргумент данного числа: r = = = 8; т. к. a = –8 < 0, то j = + p =
= + p = + p = 0 + p = p.

Тогда z ₃ = –8 = r (cos j + i × sin j) = 8(cos p + i × sin p).

г) z ₄ = –2(cos – i × sin ) = –2 cos + 2 i × sin Þ a = –2 cos , b = 2 sin . Найдем модуль и аргумент данного числа: r = = = 2; т. к. a = –2 cos < 0, то j = + p = + p = – + p = – + p = .

Тогда z ₄ = –2(cos – i × sin ) = r (cos j + i × sin j) = 2(cos + i × sin ).