Комплексные числа

Понятие числа является одним из основных завоеваний человеческой культуры. Сначала появились натуральные числа N = {1, 2, 3, …, n, …} затем целые Z = {…, –2, –1, 0, 1, 2, …}, рациональные Q = { 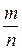| m Î Z, n Î N} (для того чтобы всякое уравнение вида а × х = b, где а ≠ 0 имело решение); потом появились иррациональные числа это было связано с решением квадратных уравнений, например х ² = 2, на множестве рациональных чисел это уравнение не имеет решения. Иррациональные числа – это бесконечные непериодические десятичные дроби, например p, е, , , …. Рациональные числа можно представить конечными или бесконечными периодическими десятичными дробями, например = 0,2; = 0,(3). Рациональные и иррациональные числа образуют множество R действительных чисел. На этом множестве уравнение х ² = 2 уже имеет два корня х ₁ = и х ₂ = – . Но действительных чисел оказалось недостаточно для того, чтобы, например решить квадратное уравнение вида х ² + 1 = 0 (т. к. на множестве действительных чисел нет такого числа, квадрат которого отрицателен). Поэтому ввели комплексные числа C. Впервые упоминание о комплексных числах появилось в работах итальянского ученого Кардано[5] в 1545 г., когда он пришел к выражению , решая кубическое уравнение х ³ –12 х + 16 = 0. Термин «комплексное число» ввел немецкий математики Гаусс[6] в 1831 г. Первоначально комплексные числа называли мнимыми. И только когда датчанин Вессель[7](1799 г.) (независимо от него француз Арган[8] (1806 г.) и немец Гаусс (1832 г.)) дал геометрическое истолкование комплексного числа, они получили признание и нашли широкое применение.

Уравнение вида х ² + 1 = 0 приводит к понятию мнимой единицы. Решая это уравнение, получаем х ² = –1 или х = 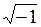; 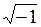назвали мнимой единицей и обозначили i = 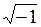или i ² = –1.

Определение 1.17. Комплексным числом называется выражение вида a + b × i, где a, b Î R, i = 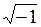– мнимая единица.

Комплексное число z = a + b × i состоит из двух частей: число а = Re z – называется действительной частью z, b = Im z – мнимой частью комплексного числа z.

Используют следующие термины: если b = 0, то a + 0× i = а – действительное число (точнее отождествляют с действительным числом), в частности 0 + 0× i = 0; если а = 0, то числа вида b × i (b ≠ 0) называют чисто мнимым. Множество всех комплексных чисел обозначают C = { a + b × i | a, b Î R, i = 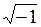} при этом R Ì C.

Определение 1.18. Комплексное число, записанное в виде z = a + b × i, называется алгебраической формой записи комплексного числа.

Определение 1.18. Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части равны, т. е. a + b × i = с + d × i Û a + с и b = d.

Определение 1.19. Комплексные числа вида a + b × i и a – b × i называются сопряженными.

Определение 1.20. Комплексные числа вида a + b × i и – a – b × i называются противоположными.