Примеры решения задач. Задача 6.3.1. Точка М движется по своей траектории согласно уравнениям

Задача 6.3.1. Точка М движется по своей траектории согласно уравнениям

х = t ² см; у = sin πt см.

Определить траекторию точки М, ее скорость и ускорение в мо­мент времени t ₁ = 1,5 с. Определить касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение. Для определения траектории точки М исключим из уравнений движения время, после чего получим уравнение тра­ектории в виде

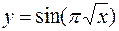
Определяем положение точки М в момент времени t ₁ (рис. 6.2)

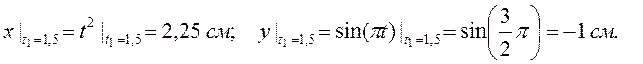
Для определения скорости точки М вычисляем первые производные от координат по времени, равные проекциям скорости точки на со­ответствующие оси координат:

.

Модуль скорости определяем по формуле

.

Вычисляем проекции вектора скорости точки на оси координат и её модуль в момент времени t ₁

Направление вектора скорости определяем при помощи направ­ляющих косинусов

В момент времени t ₁ направляющие косинусы вектора скорости

т.е. вектор скорости точки направлен параллельно оси Ох.

Для определения ускорения точки М вычисляем первые произ­водные от проекций скорости или вторые производные от координат по времени, равные проекциям ускорения точки на соответствую­щие оси координат:

.

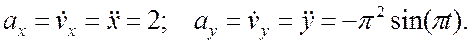Модуль ускорения определяем по формуле

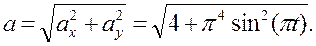
Проводим вычисления для момента времени t ₁

Направление вектора ускорения определяем при помощи на­правляющих косинусов

В момент времени t ₁ направляющие косинусы вектора ускорения

Для определения касательного ускорения 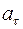точки М учтем, что его можно определить как проекцию вектора полного ускорения на направление касательной к траектории

.

В момент времени t ₁

м / с ².

Для определения нормальной составляющей вектора полного ускорения воспользуемся формулой

м / с ².

В данной задаче вектор касательного ускорения совпадает с проекцией вектора полного ускорения на ось Ох, а вектор нормаль­ного ускорения - с проекцией ускорения на ось Оу.

Радиус кривизны траектории определяем, используя формулу для вычисления нормального ускорения

.

В момент времени t ₁

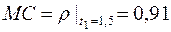м.

Изображаем все найденные величины на рис. 6.2.

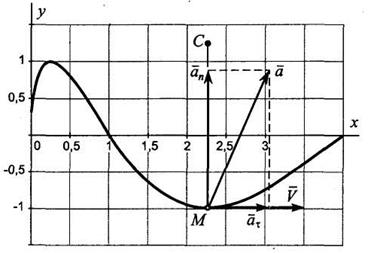
Рис. 6.2