 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Базовые понятия теории и методические рекомендации по решению задач. Кинематика — это раздел теоретической механики, в котором изучают механическое движение материальных тел без рассмотрения условий
|
|
Кинематика — это раздел теоретической механики, в котором изучают механическое движение материальных тел без рассмотрения условий, вызывающих или изменяющих это движение.
Движение материальных тел происходит в пространстве и во времени. Пространство рассматривают как трехмерное евклидово, время в этом пространстве одинаково во всех его точках и не зависит от движения материальных тел.
Под механическим движением понимают изменение положения одного тела относительно другого.
Системой отсчета называют систему координат, связанную с одним из тел. Если тело движется, то система отсчета подвижна, если тело в покое, то система отсчета неподвижна.
Основные задачи кинематики:
1. Установление закона движения тела по отношению к выбранной системе отсчета.
2. Определение по заданному закону движения тела кинематических характеристик этого движения: траектории, скорости, ускорения, угловой скорости и ускорения и т. д.
Движение точки считают заданным, если известен способ, позволяющий установить ее положение относительно выбранной системы отсчета в любой момент времени.
Существуют три способа задания движения точки: векторный, координатный, естественный.
Векторный способ задания движения заключается в задании положения точки радиусом-вектором, который является векторной функцией времени, относительно выбранной точки отсчета.
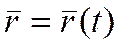 .
.
Траектория точки М при векторном способе — это геометрическое место точек концов радиуса-вектора 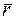 при изменении времени, т. е. годограф радиуса-вектора.
при изменении времени, т. е. годограф радиуса-вектора.
Годограф — это кривая, которую описывает конец радиуса-вектора при изменении его аргумента, когда начало вектора находится в одной и той же точке.
Скорость точки характеризует быстроту и направление движения точки и равна производной радиуса-вектора точки по времени:
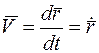 .
.
В механике производную по времени обозначают точкой над переменной.
Вектор скорости точки направлен по касательной к траектории точки в сторону ее движения.
Ускорение точки характеризует быстроту изменения величины и направления скорости точки и равно первой производной вектора скорости по времени или второй производной радиуса-вектора по времени:
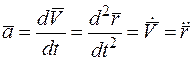 .
.
Вектор ускорения направлен по касательной к годографу вектора скорости.
Координатный способ задания движения заключается в задании координат точки в виде известных, непрерывных, дважды дифференцируемых функций времени.
В декартовой системе координат уравнениями движения точки будут
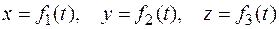 .
.
Скорость точки в декартовых координатах:
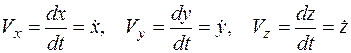 ,
,
где 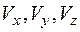 — проекции вектора скорости на соответствующие оси координат;
— проекции вектора скорости на соответствующие оси координат;
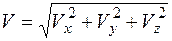 .
.
Углы вектора скорости с осями координат:
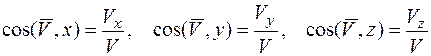 .
.
Ускорение точки в декартовых координатах:
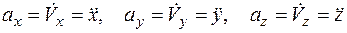 ,
,
(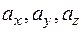 — проекции вектора ускорения на соответствующие оси координат):
— проекции вектора ускорения на соответствующие оси координат):
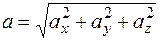 .
.
Углы вектора ускорения с осями координат:
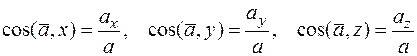 .
.
Естественный способ задания движения считается известным, если заданы:
1. Траектория точки.
2. Закон движения точки по траектории 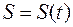 .
.
3. Начало отсчета.
4. Положительное и отрицательное направления движения.
Закон движения 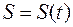 также называют дуговой координатой, которую отсчитывают от начального положения. Дуговую координату не следует смешивать с длиной пути, пройденного точкой, так как за начало отсчета может быть выбрана любая точка или движение может быть колебательным.
также называют дуговой координатой, которую отсчитывают от начального положения. Дуговую координату не следует смешивать с длиной пути, пройденного точкой, так как за начало отсчета может быть выбрана любая точка или движение может быть колебательным.
При естественном способе задания движения точки в качестве координатных осей принимают естественные оси (оси естественного трехгранника): 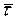 — касательная,
— касательная, 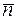 — нормаль,
— нормаль, 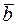 — бинормаль.
— бинормаль.
Скорость точки 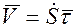 ,
,
или
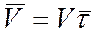 .
.
Ускорение точки
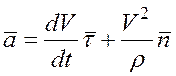 .
.
Ускорение точки состоит из двух взаимно перпендикулярных
составляющих. Одна 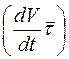 направлена по касательной к траектории, а другая
направлена по касательной к траектории, а другая 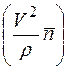 - по нормали к этой траектории в сторону ее вогнутости. Эти составляющие называют соответственно касательным и нормальным ускорениями точки. Они лежат в соприкасающейся плоскости. Проекция ускорения точки на бинормаль равна нулю, так как вектор ускорения расположен в соприкасающейся плоскости (рис. 6.1):
- по нормали к этой траектории в сторону ее вогнутости. Эти составляющие называют соответственно касательным и нормальным ускорениями точки. Они лежат в соприкасающейся плоскости. Проекция ускорения точки на бинормаль равна нулю, так как вектор ускорения расположен в соприкасающейся плоскости (рис. 6.1):
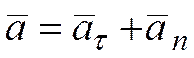 .
.
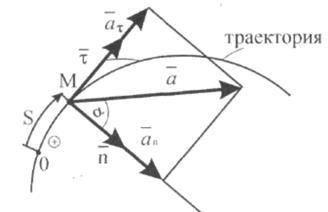
Рис. 6.1
Вектор касательного ускорения
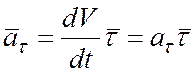 ,
,
модуль касательного ускорения
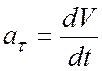 .
.
 Вектор нормального ускорения
Вектор нормального ускорения
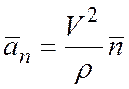 ,
,
модуль нормального ускорения
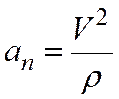 .
.
Модуль ускорения равен:
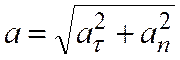 .
.
Угол отклонения вектора ускорения от нормали составит (рис. 6.1):
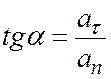 .
.
Дата публикования: 2014-11-18; Прочитано: 1160 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
