Направленные ответвители с многими направленными элементами связи

Методы расчета направленных ответвителей с нена­правленными элементами связи, изложенные в предыду­щих разделах, при определенных дополнительных усло­виях могут быть применены и в том случае, когда эле­менты связи обладают собственной направленностью *.

Рассмотрим возможность применения чебышевского распределения к «риблетовским» элементам связи, кото­рые часто применяются в конструкциях направленных ответвителей со связью по широкой стенке волновода с доминантной волной TE₀₁ [13, 14]. Широкое использова­ние «риблетовских» элементов связи объясняется высо­ким постоянством их переходного ослабления в достаточ­но широком диапазоне, а также высокой прямой собст­венной направленностью, что позволяет получать высо­кую направленность ответвителя в диапазоне с относи­тельно небольшим числом элементов связи.

Используя выражение (17), получим соотношения, определяющие все свойства «риблетовского» элемента связи:

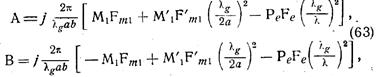
откуда собственная направленность элемента связи

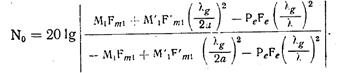(64)

Собственная направленность «риблетовского» эле­мента связи максимальна, если амплитуда В=0, что соответствует длине волны λ₀. которая определяется со­отношением:

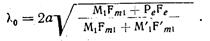(65)

Проведем анализ при предположениях, что размеры эле­ментов связи много меньше длины волны в волноводе а толщина общей стенки мала, то есть коэффициенты за­тухания F _m = F _e ≈l.

При распределении амплитуд волн, возбуждаемых «риблетовскими» элементами связи во вспомогательном волноводе, необходимо учитывать следующее:

а) Величина собственной направленности каждого элемента связи зависит от размеров составляющих эле­ментов (продольной и поперечной щелей) l ₁, l ₂, ω ₁, ω ₂. Та­ким образом, если менять ослабление отдельных элемен­тов по какому-либо закону, то одновременно будет изме­няться и собственная направленность каждого элемента;

б) длина волны λ₀, соответствующая максимальной собственной направленности для каждого элемента свя­зи, существенно зависит от его размеров, а следователь но, при распределении переходного ослабления отдель­ных элементов максимальная направленность у каждого элемента связи будет достигаться на своей длине волны и меняться по своему закону, зависящему от размеров отверстия связи.

Из соотношений (64) и (65) видно, что зависимость N₀ и λ₀ от размеров элементов связи l ₁, l ₂, ω ₁, ω ₂ заклю­чена в коэффициенты М и Р, которые входят линейно во все слагаемые числителя и знаменателя. Обычно l ₁= l ₂ и ω ₁= ω ₂, поэтому коэффициенты поляризации зависят от двух переменных l и ω. Если положить l = kω, то полу­чим:

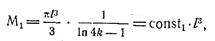(66)

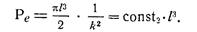(67)

Тогда выражения (64) и (65) примут вид:

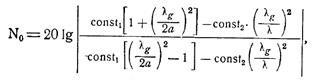(68)

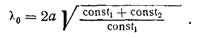(69)

Таким образом, в рамках, сделанных предположений направленность «риблетовских» элементов связи, для ко­торых при различных переходных ослаблениях выполня­ется условие l_i = kω_i, не зависит от l и ω, то есть все эле­менты связи имеют одинаковую величину направленно­сти и соответствующую ее максимуму, общую для всех; длину волны.

При этих условиях расчет ответвителя с «риблетов­скими» элементами связи аналогичен расчету ответвите­ля с ненаправленными элементами связи. Но посколь­ку «риблетовский» элемент связи обладает высокой соб­ственной направленностью, то его можно рассматривать и как элементарный ответвитель. Тогда для совокупности m «риблетовских» элементов связи справедливы все по­ложения каскадного соединения направленных ответвителей, расположенных на расстоянии λ_g0/4 друг от друга.

Переходное ослабление отдельного элемента связи ответвителя, состоящего из m «риблетовских» элементов 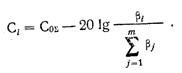(70)

Выражение для направленности ответвителя с уче­том собственной направленности элементов связи, рав­ной для всех элементов, имеет вид:

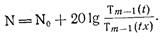(71)

Рассмотрим, что дает применение чебышевского рас­пределения амплитуд волн, возбуждаемых «риблетовскими» элементами связи, по сравнению с обычно ис­пользуемым однородным распределением (стр. 49).

В случае применения направленного ответвителя с однородным распределением «риблетовских» элементов связи выражение для направленности с учетом (46) за­пишется в виде:

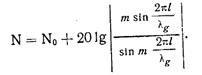(72)

Минимальное значение направленности для ответви­теля с чвбыш'ввским распределением соответствует tx =1 при котором амплитуда обратной волны во вспомогатель­ном волноводе

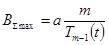. (73)

В случае однородного распределения выражение (73) примет вид:

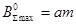, (74)

откуда выигрыш распределения очевиден и выражается соотношением:

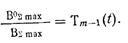
Экспериментальные ответвители чебышевского типа с «риблетовским» элементами связи имеют направлен­ность N>35 дб в полосе 36%. переходное ослабление C_0Σ = 20±0,5 дб при числе элементов связи m =10.