Направленности

Итак, в предыдущих разделах было показано, что для работы направленного ответвителя интерференционного типа с числом элементов связи более двух необходимо, чтобы величины амплитуд электромагнитных волн, воз­буждаемых отверстиями связи, подчинялись какому-либо закону с условием В_Σ=0 при l =λ_g/4, где λ_g/4 – дли­на волны в волноводе, В_Σ – суммарная амплитуда электромагнитной волны в обратном направлении (пря­мым направлением считаем направление распростране­ния электромагнитной волны в основном волноводе).

Направленный ответвитель, очевидно, будет идеаль­ным, если в некотором диапазоне длин волн в выражении направленности величина B_Σ=0. По­этому вопрос об оптимальной направленности ответ­вителя в диапазоне длин волн сводится к вопросу о наилучшей аппроксимации некоторой заданной функ­ции.

В данном случае аппроксимирующая функция равна величине амплитуды суммарной волны в обратном на­правлении, аппроксимируемая – нулю, интервал аппрок­симации –λ₁≤λ≤λ₂.

Аппроксимация Гаусса. Приближение считается до­статочно хорошим, если интеграл квадрата уклонения данной функции g(x) от другой функции, выбранной со­ответствующим образом из семейства функций в интервале a ≤ x ≤ b

принимает минимальное значение относительно возмож­ных вариаций параметров a ₁.

Аппроксимация Чебышева требует, чтобы максимум абсолютного значения уклонения был возможно малым, то есть максимум величины был возможно малым в интервале a ≤ x ≤ b.

Так как в направленном ответвителе величина направленности определяется не средним, а наибольшим значением квадрата уклонения, то лучше использовать аппроксимацию Чебышева [21, 22].

Рассмотрим направленный ответвитель интерферен­ционного типа (рис. 24) с семью отверстиями связи, рас­стояние между которыми равно l.

Если предположить, что система отверстий ответвителя симметрична относи­тельно среднего отверстия связи, то отверстия возбуж­дают во вспомогательном волноводе II электромагнит­ные волны с соответствующими амплитудами А₃, А₂, A₀, A₁, A₂, A₃.В дальнейшем считаем, что ослабление волны основного волно­вода I за счет ответвления мало и элементы связи нена­правленные.

Пусть A_Σ и B_Σ – амплитуды суммарных волн в вол­новоде II соответственно в прямом и обратном направлениях. Для них справедливы соотношения:

При исследовании оптимальности характеристики на­правленности ответвителя основной интерес представля­ет выражение для B_Σ. Если в вышенаписанном выраже­нии положить cos φ = х, то

Выражение (48) полностью совпадает с выражением для входного коэффициента отражения шестиступенчатого перехода, полученного в работе [21].

где Г_вх – входной коэффициент отражения, Г _i – отражения от ступеней перехода.

Это указывает на то, что расчет ступенчатого перехо­да и расчет направленного ответвителя интерференцион­ного типа аналогичны.

Выражение в квадратных скобках соотношения (48) –действительное число. Поскольку А _i (i = 0, 1, 2, 3) заранее не определены, то вышенаписанный полином можно приравнять к любому полиному третьей степени от tx (t – масштабный множитель по оси х) с любыми наперед заданными постоянными коэффициентами. Если учесть, что у полиномов Чебышева все корни действи­тельные и что именно полиномы Чебышева обеспечива­ют наименьшее отклонение от нуля в интервалах между корнями, то выражение B_Σ необходимо приравнять к по­линому Чебышева третьей степени.

Решив систему линейных уравнений, полученных or приравнивания друг к другу коэффициентов при одинако­вых степенях х, получим [21]. А₀ = 0; А₂ = 0;

где T₃*(t)= ,

T₃*(t) = 4 t ³–3 t – ненормированный полином Чебы­шева первого рода третьей сте­пени,

М – величина амплитуды обратной волны в случае отсутствия на­правленности, то есть М=|A_Σ|. Таким образом, из семи отверстий связи в формирова­нии направленности участвуют только четыре отверстия, а именно: отверстия, возбуждающие во вспомогатель­ном волноводе волны с амплитудами А₃, А₁ А₁ А₃. Расстояние между отверстиями связи также изменилось и стало вдвое больше прежнего, то есть L = 2 l.

Проводя соответствующие выкладки, можно показать что

где λ_{g min} и λ_{g max} – граничные длины волн заданного диапазона.

Обобщая полученный результат на случай направ­ленного ответвителя с n +1 отверстием связи, получим:

(50)

При расчете направленного ответвителя с чебышевским распределением нет необходимости опреде­лять амплитуды волн, возбуждаемых каждым элементом связи, подобно тому, как они определялись выше. Расчет направленного ответвителя значительно упрощается, если пользоваться обобщенным треугольником коэффи­циентов распределения для полиномов Чебышева первого рода [47, 23]. Обобщенный треугольник приведен в таб­лице 2.

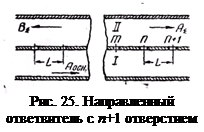
Если теперь вновь пронумеровать отверстия связи так, как показано на рис. 25, то для величин амплитуд волн, возбуждаемых во вторичном волноводе отверстия­ми связи, будут справедливы следующие соотношения:

(51)

где а_m – коэффициент m -го столбца и n -й строки обоб­щенного треугольника коэффициентов распре­деления для полиномов Чебышева первого рода. Введем понятие выигрыша направленного ответви­теля, который определяется выражением:

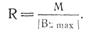(52)

Учитывая, что М=|A_Σ|, выражение (52) примет вид:

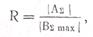
откуда минимальная направленность ответвителя

(53)

Таким образом, выигрыш направленного ответвителя определяет минимальную величину направленности от­ветвителя в рабочем диапазоне длин волн. Понятие выигрыша может быть использовано при любом законе распределения амплитуд волн, возбуждаемых отверсти­ями связи во вспомогательном волноводе.

Сравним выигрыши чебышевского и биноминального направленных ответвителей при одинаковом количестве отверстий связи и одинаковом коэффициенте перекры­тия. Для биноминального направленного ответвителя . Величина х достигает максимального значения на краях диапазона, то есть при х=1/ t поэто­му

Ввиду того, что R_чеб=Т n (t), а по известному свойст­ву полиномов Чебышева, если t>1, то Т n (t)>tⁿ, по­лучим R_чеб> R_бин. Следовательно, минимальная на­правленность ответвителя, рассчитанного с применением полиномов Чебышева (чебышевской аппроксимации), превосходит минимальную направленность ответвителя c биноминальным распределением амплитуд волн, воз­буждаемых отверстиями связи во вспомогательном волно­воде. При одинаковом значении N_min в рабочем диапа­зоне длин волн чебышевский направленный ответвитель имеет более широкий рабочий диапазон волн, чем бино­минальный.

Обычно при расчете направленного ответвителя зада­ют рабочий диапазон длин волн λ₁≤ λ≤ λ₂, переходное ослабление ответвителя и минимальную направленность в диапазоне

Не снижая общности расчета, можно считать, что в основном волноводе распространяется волна единичной амплитуды. Тогда из формулы для переходного ослабле­ния следует, что

Итак, для расчета направленного ответвителя чебы­шевского типа (и не только чебышевского типа) необ­ходимо задать рабочий диапазон длин волн, переходное ослабление и минимальную направленность в диапазо­не. По формулам (49) определить величины q и t. Опре­делить число элементов связи, используя неравенство

Найти величины амплитуд волн, воз­буждаемых каждым отверстием связи по соотношениям (51). По найденным значениям A _m определить распреде­ление переходного ослабления по отверстиям связи, ис­пользуя соотношение 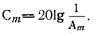Наконец, вычислить размеры элементов связи, пользуясь для каждого кон­кретного случая конфигурации отверстия соответствую­щими формулами предыдущих разделов.