 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Аналогові та цифрові сигнали
|
|
До основних типів відносять аналоговий, дискретний і цифровий сигнали.
Аналоговим називають сигнал, неперервний у часі і значеннях. Такий сигнал описується неперервною або кусочно неперервною функцією f(t) при цьому і аргумент і функція можуть приймати довільні значення.  ;
; 
Приклад:
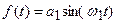
 - гармонійне коливання;
- гармонійне коливання;
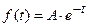
 - експонента.
- експонента.
Дискретизований – сигнал, дискретний у часі і неперервний у значенні. Такий сигнал описується решітчастою функцією – послідовністю  , яка визначена тільки в конкретні значення аргументу і може приймати довільні значення. Графік дискретизованого сигналу наведений на рис.1.2.
, яка визначена тільки в конкретні значення аргументу і може приймати довільні значення. Графік дискретизованого сигналу наведений на рис.1.2.
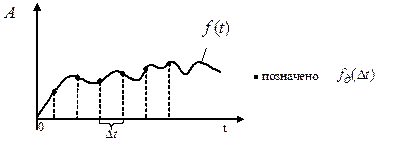
Рис. 1.2. Графік дискретизованого сигналу
Цифровий сигнал – це дискретизований сигнал, який набуває значень зі скінченої кількості рівнів квантування. Такий сигнал описується квантованою решітчастою функцією – квантованою послідовністю 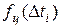 , відліки якої в кожен момент часу набувають дискретне значення рівнів квантування. Графік цифрового сигналу наведений на рис.1.3.
, відліки якої в кожен момент часу набувають дискретне значення рівнів квантування. Графік цифрового сигналу наведений на рис.1.3.

Рис.1.3. Графік цифрового сигналу
Цифрові сигнали формуються з аналогових за два етапи. Перший з них – дискретизація, другий – квантування.
Дискретизація
Дискретизація – це послідовне вимірювання амплітудних значень сигналу через певні інтервали часу Dt (при цьому отримуються послідовні відліки 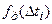 ). Надалі мова піде про рівномірну дискретизацію, при якій інтервал часу Dt не змінюється. Умови, за яких можливе повне відновлення аналогового сигналу за його цифровим еквівалентом зі збереження всієї вхідної інформації, що містилася в сигналі, виражаються теоремами Котельникова, Найквіста, Уіттекера, Шеннона, сутність яких практично однакова.
). Надалі мова піде про рівномірну дискретизацію, при якій інтервал часу Dt не змінюється. Умови, за яких можливе повне відновлення аналогового сигналу за його цифровим еквівалентом зі збереження всієї вхідної інформації, що містилася в сигналі, виражаються теоремами Котельникова, Найквіста, Уіттекера, Шеннона, сутність яких практично однакова.
Для того, щоб перейти до розгляду теореми дискретизації необхідно визначити такі поняття: частота;частотний спектр; ширина частотної смуги; частотний діапазон.
Часова область. Часова область зручна при зображенні змін сигналу в часі. Ми всі знаємо, що таке синусоїди. Кожна синусоїда характеризується трьома параметрами: амплітудою, початковою фазою і частотою. Одна синусоїда має одну частоту. Частота - це параметр, що показує як часто сигнал повторює сам себе. Зворотним до частоти є період. Він відповідає тривалості, що займає в часі один період періодичного сигналу. На рис.1.4.а наведені графіки сигналів в часовій області (синусоїди з. з різними частотами і, отже, різними періодами).
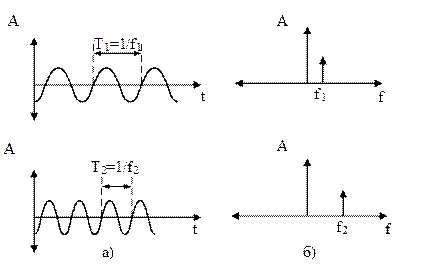
Рис.1.4. Графіки сигналів в часовій та частотній областях
Синусоїда описується формулою 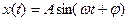 , де
, де 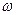 - кругова частота (вимірюється в радіанах). Формула зв’язку між круговою і лінійною (вимірюється в Герцах) частотою:
- кругова частота (вимірюється в радіанах). Формула зв’язку між круговою і лінійною (вимірюється в Герцах) частотою: 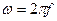 .
.
Частотна область. Частотна область зручна при зображенні частотного складу сигналів. Кожна синусоїда, що наведена на рис.1.4.а, має одну частоту. Отже, у частотній області кожна синусоїда представляється тільки однією частотною складовою. Її амплітуда у частотній області (на рис.1.4.б - пряма зі стрілкою нагору) пропорційна амплітуді синусоїди в часовій області. Частота f1 відповідає частоті першої синусоїди, а f2 - другої. Чим вища частота синусоїди, тим далі вправо, відносно нульового значення частоти, по осі частот вона розташовується. (Словосполучення “частотна складова” для стислості заміняють на «частоту», якщо зрозуміло, що мова йде про складову частотного спектра, а не про поняття частоти як такої).
Реальні сигнали є комбінацією множини синусоїд з різними частотами, амплітудами і початковими фазами..
Спектр (частотний) сигналу відображає його точний частотний склад.
Частотний діапазон, або смуга частот це - проміжок між мінімальною та максимальною частотою, що наявні в сигналі.
Ширина смуги сигналу - це різниця між його найвищою і найнижчою частотами, при яких амплітуди перевищують задане значення.
Підкреслимо різницю між шириною смуги і частотним спектром. Ширина смуги сигналу дає нам інформацію про розмах (ширину) частотного діапазону сигналу. Спектр сигналу відображає його точний частотний склад. Можна мати два сигнали з однаковою шириною смуги 10 кГц, але один, розташований у діапазоні від 5 кГц до 15 кГц, а іншої - у діапазоні від 500 кГц до 510 кГц. Виходить, ширина смуги не дає інформації про значення частот, що втримуються в сигналі. Спектр же сигналу дозволяє їх побачити. Таким чином, два сигнали з однаковою шириною смуги можуть мати два зовсім різних спектри.
Теорема Котельникова
Якщо сигнал  обмежений смугою
обмежений смугою  , то він може бути відтворений з як завгодно великою точністю за відліками, що взяті з частотою дискретизації
, то він може бути відтворений з як завгодно великою точністю за відліками, що взяті з частотою дискретизації  :
:
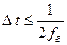 чи
чи 
Тобто, якщо сигнал має спектр, обмежений частотою fг то після дискретизації сигналу з частотою не менше 2fг можна відновити вхідний неперервний сигнал за отриманим цифровим значенням абсолютно точно
Якщо умова теореми Котельникова порушується, у цифровому сигналі виникає ефект маскування (підміни) дійсних частот "гаданими" більше низькими частотами. Цей ефект також називають накладанням спектрів, або елайсингом (aliasing).
Для того, щоб уникнути накладання спектрів можна використовувати більш високу частоту дискретизації. Проте вибір надто малого 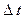 приводить для надлишковості обчислень.
приводить для надлишковості обчислень.
Квантування
Квантування проводиться з метою представлення точних значень сигналу (відліків) у вигляді двійкових чисел скінченої розрядності – цифрових відліків  . Для цього динамічний діапазон дискретного сигналу розбивається на скінчену кількість дискретних рівнів – рівнів квантування - і кожному відліку за певним правилом присвоюється значення одного з найближчих рівнів. Рівні квантування кодуються двійковими числами, що мають розрядність b, яка залежить від кількості рівнів квантування R:
. Для цього динамічний діапазон дискретного сигналу розбивається на скінчену кількість дискретних рівнів – рівнів квантування - і кожному відліку за певним правилом присвоюється значення одного з найближчих рівнів. Рівні квантування кодуються двійковими числами, що мають розрядність b, яка залежить від кількості рівнів квантування R:
R≤2b.
Звідси випливає, що b=[log2R], де [] – ціле значення, отримане методом заокруглення до більшого.
Наприклад, якщо обрано 5 рівнів квантування (без врахування знаку), то відліки будуть кодуватися 4-розрядними двійковими числами (b=[log25=3]): один розряд знаковий і три значущих.
Сукупність квантованих відліків 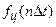 , n=0,1,... називають, як було вже згадано, цифровим сигналом.
, n=0,1,... називають, як було вже згадано, цифровим сигналом.
Відстань між двома сусідніми рівнями квантування називається кроком квантування.
Квантування приводить до появи похибки квантування (eкв), оскільки має місце операція зоокруглення.
eкв = fц - fд
Квантування, як і дискретизація реалізовуються за допомогою АЦП..
Для того щоб оцінити вплив перешкоди, вводиться поняття “ відношення сигнал-шум ” - відношення потужності сигналу до потужності шуму (у децибелах).
 (дБ)
(дБ)
Найчастіше використаються 8-, 10-, 12-, 16-, 20- і 24-х розрядні АЦП. Кожен додатковий розряд покращує відношення сигнал-шум на 6 децибел. Проте збільшення кількості розрядів знижує швидкість дискретизації і збільшує вартість апаратури.
Дата публикования: 2014-11-18; Прочитано: 8994 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
