Правильні області

Для довільної області D процес складання інтегральної суми та знаходження

значення подвійного інтеграла як границі інтегральної суми є досить складним. Розглянемо більш прості види областей на евклідовій площині.

Області правильні в напряму координатних осей

Рис.1.8	D: (1.7) Криві , обмежують область в напряму осі ОУ.
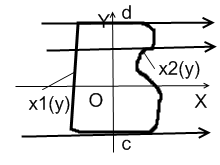Рис. 1.9	D: (1.8) Криві , обмежують область в напряму осі OX.
Рис.1.10	Область довільної форми можна розглядати як об'єднання скінченної кількості правильних областей (рис.1.10), які не мають спільних внутрішніх точок. Області А, В та С правильні в напряму координатної осі ОУ.

а) Область D є правильноюв напряму координатної осі OY, якщо будь-яка пряма паралельна до цієї осі перетинає межі області не більше як в двох точках (рис.1.8). Область D правильну в напряму осі OY можна описати аналітично системою нерівностей, формула (1.7).

б) Область D є правильною в напряму осі OX, якщо будь-яка пряма паралельна

до осі OX перетинає межі області не більше як в двох точках (рис.1.9). Таку

область можна описати аналітично системою нерівностей, формула (1.8).