 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Подвійний інтеграл
|
|
Знайдемо границю подвійної інтегральної суми при 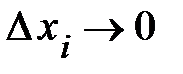 ,
, 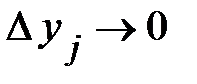 . Якщо вона існує, позначимо її:
. Якщо вона існує, позначимо її:
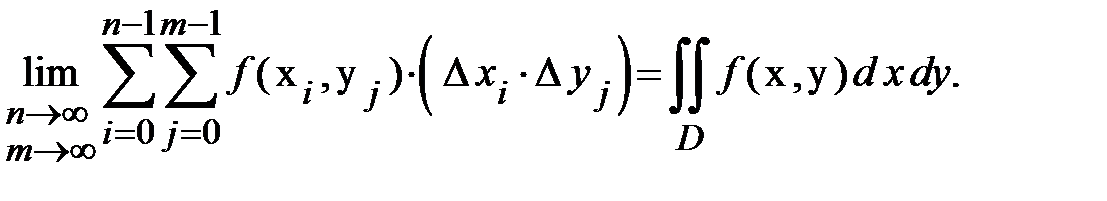 (1.4)
(1.4)
Повернемось до інтегральної суми 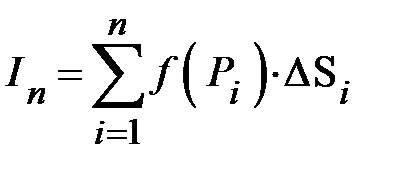 . Позначимо найбільшу з елементарних площ
. Позначимо найбільшу з елементарних площ 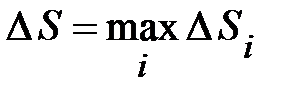 ,
, 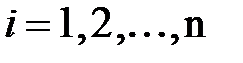 .
.
Якщо інтегральна сума при 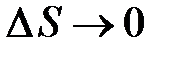 має границю,
має границю,
 (1.5)
(1.5)
яка не залежить ні від способу розбиття області D на частини 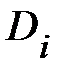 , ні від вибору точок
, ні від вибору точок 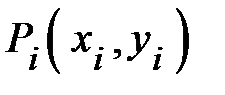 ,
, 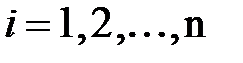 , в цих частинах, то ця границя називається подвійним інтегралом по області
, в цих частинах, то ця границя називається подвійним інтегралом по області  і позначається
і позначається
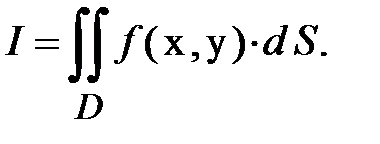 (1.6)
(1.6)
Якщо існує границя інтегральної суми функції 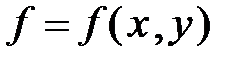 , то функція
, то функція 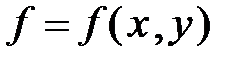 називається інтегровною в області D; D – область інтегрування; х, у – змінні інтегрування;
називається інтегровною в області D; D – область інтегрування; х, у – змінні інтегрування; 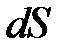 (або
(або 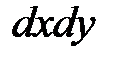 ) – елемент площі.
) – елемент площі.
Теорема 1.1. (достатні умови інтегровності функції).
Якщо функція 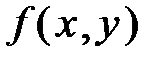 неперервна в замкненій квадровній області D, то вона інтегровна в цій області. Таким чином, існує границя інтегральної суми, формула (1.5), яка не залежить ні від способу розбиття області D на частини
неперервна в замкненій квадровній області D, то вона інтегровна в цій області. Таким чином, існує границя інтегральної суми, формула (1.5), яка не залежить ні від способу розбиття області D на частини 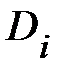 , ні від вибору проміжних точок
, ні від вибору проміжних точок 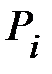 в цих частинах.
в цих частинах.
Обидві границі, формули (1.4) і (1.5), відповідають точному значенню шуканої величини F. Отже справедлива рівність:
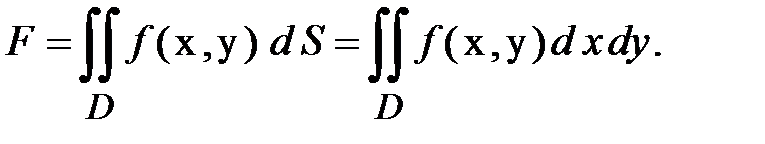
Дата публикования: 2014-11-18; Прочитано: 441 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
