 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Геометричний зміст подвійного інтеграла
|
|
1.1. За допомогою подвійних інтегралів обчислюють об’єм циліндричних тіл, при умові, що підінтегральна функція невід’ємна  в області D. При складанні інтегральної суми вважають, що значення функції
в області D. При складанні інтегральної суми вважають, що значення функції  (висота тіла
(висота тіла  ) в межах елементарної частини розбиття
) в межах елементарної частини розбиття  області інтегрування D є сталою (рис. 12), тому об’єм елементарного тіла можна обчислити за формулою об’єму паралелепіпеда,
області інтегрування D є сталою (рис. 12), тому об’єм елементарного тіла можна обчислити за формулою об’єму паралелепіпеда,  .
.
Об’єм всього циліндричного тіла, обмеженого зверху деякою поверхнею, дорівнює границі інтегральної суми:
 .
.
 Рис.13
Рис.13
| Приклад 1.3. Об’єм циліндричного тіла (рис.13),
обмеженого зверху поверхнею 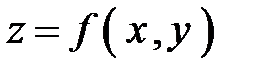 , знизу площиною , знизу площиною  , з боку циліндричною поверхнею , з боку циліндричною поверхнею  , де , де  – рівняння межі області інтегрування D в площині ХОУ, дорівнює подвійному інтегралу – рівняння межі області інтегрування D в площині ХОУ, дорівнює подвійному інтегралу
 .
Межа області інтегрування є напрямною циліндричної поверхні, твірна якої паралельна до осі OZ. .
Межа області інтегрування є напрямною циліндричної поверхні, твірна якої паралельна до осі OZ.
|
1.2.Якщо підінтегральна функція є сталою і дорівнює одиниці,
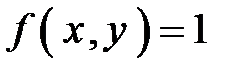 , то значення подвійного інтеграла чисельно дорівнює площі області інтегрування D:
, то значення подвійного інтеграла чисельно дорівнює площі області інтегрування D:
 .
.
Дата публикования: 2014-11-18; Прочитано: 3268 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
