Підстановки n-го степеня

Означення. Підстановкою 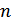-го степеня називається бієктивне відображення 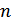-елементної множини у себе.

Будемо записувати підстановку у два рядки: у першому будуть вихідні 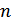елементів, а у другому – їх образи.

Наприклад:

Поставимо 2 питання:

1) Скільки форм запису однієї ї тієї підстановки.

2) Скільки різних підстановок n-го степеня можна скласти.

На обидва питання відповідь: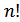

Розглянемо перше питання. Різні форми запису можна отримати за рахунок різного розташування стовпчиків перестановок. З теорії перестановок відомо, що їх буде n!.

Розглянемо друге питання. Зафіксуємо елементи у першому рядку. Очевидно, що підстановки будуть різними, якщо відрізняються відповідно образи у другому рядку. Отже кількість підстановок дорівнюватиме кількості перестановок елементів другого рядка, а їх, як відомо, n!.

Означення. Підстановка називається парною, якщо парності верхньої і нижньої перестановок однакові, тобто обидві перестановки або парні або непарні.

Означення. Підстановка називається парною, якщо загальна кількість інверсій верхньої і нижньої перестановок є парним числом, в супротивному разі перестановка непарна.

Теорема. При n≥2 кількість парних підстановок дорівнює кількості непарних підстановок, тобто дорівнює .

Запишемо всі підстановки у вигляді:

Твердження теореми випливає з відповідної теореми для перестановок. Дійсно, тоді парність підстановки визначається лише парністю нижньої перестановки, а парних нижніх існує .

Зауваження. Для самостійного доведення залишається факт, що означення парності підстановки не залежить від форми запису цієї підстановки.