Перестановки з nсимволів

Означення 1. Перестановкою з 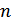символів називається розташування цих символів в деякому порядку.

Означення 2. Транспозицією називається таке перетворення перестановки, при якому два її елементи міняються місцями.

Теорема 1. З 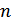символів можна скласти 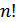перестановок.

Доведення.

Застосуємо метод математичної індукції по кількості символів n.

1. При 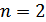це твердження є правильним, бо маємо дві перестановки: 1 2, 2 1.

2. Зробимо індуктивне припущення: з символів можна скласти перестановок.

3. Покажемо справедливість індуктивного переходу для .

Розглянемо всі перестановки з символів за такою схемою. Запишемо спочатку всі перестановки, що починаються з одних одиниць.

Ця група знаходиться в умовах індуктивного припущення. За індуктивним припущенням з символів утворюється перестановок.

Запишемо всі перестановки, що починаються з двійки, трійки, тощо.

Останньою буде група перестановок, що починаються з .

Таким чином всі перестановки розбиваються на k+1 клас, в кожний з яких входить k перестановок. Отже всього буде k!(k+1)=1ˑ2ˑ…ˑkˑ(k+1)=(k+1)! перестановок. З доведеного за принципом математичної індукції дане твердження є правильним при довільному натуральному .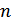

Теорема 2. Усі 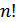перестановок з 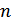символів можна записати таким списком, в якому кожна наступна перестановка може бути отримана з попередньої шляхом однієї транспозиції.