Поняття вектора, лінійні операції над векторами

Розглянемо в просторі (на площині) множину всіх направлених відрізків. В цій множині можна по-різному ввести означення рівності напрямленнях відрізків і отримати три поняття вектора.

Означення 1. Два напрямлених відрізки називаються рівними, якщо:

1) вони колінеарні (знаходяться на одній або паралельних прямих);

2) мають однаковий напрямок;

3) мають однакові довжини.

Означення 2. Вільним вектором називається множина всіх рівних між собою в сенсі означення 1 напрямлених відрізків.

Введемо іншим чином означення рівності.

Означення 1^'. Два напрямлених відрізки називаються рівними, якщо:

1) вони колінеарні;

2) мають однаковий напрямок;

3) знаходяться на одній прямій;

4) мають однакові довжини.

Означення 2^'. Ковзним вектором називається множина всіх рівних між собою у сенсі означення 1^' напрямлених відрізків.

Означення 1^''. Два напрямлених відрізки називаються рівними, якщо:

1) в них рівні довжини;

2) знаходяться на одній прямій;

3) однаково направлені і мають спільний початок.

Означення 2^''. Зв'язаним вектором називається множина рівних між собою в сенсі означення 1 ^'' напрямлених відрізків.

З останнього означення випливає, що зв'язаний вектор дорівнює лише собі. В даному курсі розглядатимемо лише вільні вектори.

Над векторами вводяться дві основні лінійні операції:

1) додавання векторів;

2) множення вектора на число.

Означення 3. Сумою двох векторів і , називається вектор, що умовно позначається , початок якого знаходиться в початку вектора , кінець – у кінці вектора , за умови, що початок вектора знаходиться в кінці вектора .

Означення 4. Добутком вектора а на число к називається вектор, що умовно позначається і має такі властивості:

1)

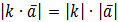
2) , якщо , і , якщо

3) не має певного напрямку, якщо .

Властивості лінійних операцій (довести самостійно).

1. – комутативність додавання.

2. – асоціативність додавання.

3. Існує так званий нульовий вектор , тобто такий, для якого

для довільного вектора .

Зрозуміло, що початок і кінець нульового вектора збігаються, тобто він має нульову довжину, а напрямок цього вектора невизначений.

4. Для будь-якого вектора існує так званий протилежний вектор , тобто такий, що .

Вектори та мають протилежні напрямки та однакові довжини.

5. для довільного вектора .

6. – асоціативність множення на число.

7. – дистрибутивність.

8. – дистрибутивність.