 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Оператор Гамильтона. Оператор Лапласа
|
|
Операции получения градиента, дивергенции и ротора можно записать более просто, если ввести в рассмотрение (чисто формально) символический вектор
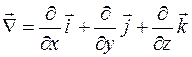 . (2.26)
. (2.26)
Символ 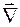 читается "набла". Этот вектор называется оператором Гамильтона* или набла-вектором. При этом формальное умножение любого из символов
читается "набла". Этот вектор называется оператором Гамильтона* или набла-вектором. При этом формальное умножение любого из символов 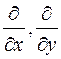 или
или 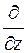 на скаляр надо понимать, как взятие частной производной по соответствующей переменной (мы об этом говорили, когда вычисляли ротор). Например,
на скаляр надо понимать, как взятие частной производной по соответствующей переменной (мы об этом говорили, когда вычисляли ротор). Например,
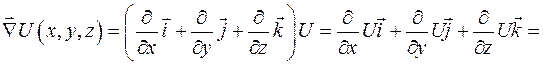
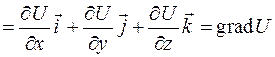 .
.
Работая с вектором 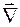 формально как с вектором, только заменяя произведение на взятие частной производной, можно вычислить скалярное и векторное произведение вектора
формально как с вектором, только заменяя произведение на взятие частной производной, можно вычислить скалярное и векторное произведение вектора 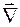 на вектор
на вектор  . Тогда получим
. Тогда получим
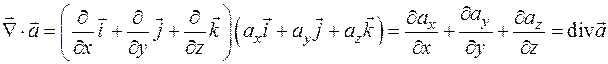 ,
,
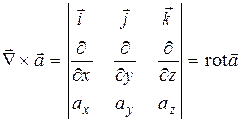 .
.
Операции получения градиента, дивергенции и ротора называются векторно-дифференциальными операциями первого порядка, так как при этом используются частные производные первого порядка.
При действиях с оператором 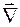 надо пользоваться правилами векторной алгебры и правилами дифференцирования. Например,
надо пользоваться правилами векторной алгебры и правилами дифференцирования. Например,
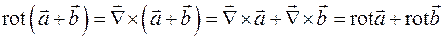 ,
,
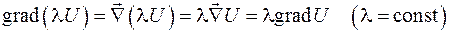 .
.
После применения оператора (2.26) к векторному или скалярному полю мы получаем новое поле, к которому опять можно применить этот оператор. Применение двух векторно-дифференциальных операций повторно называется векторно-дифференциальной операцией второго порядка.
Конечно, не всякие комбинации имеют смысл, например, комбинация  не имеет смысла, так как
не имеет смысла, так как 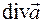 образует скалярное поле, от которого нельзя взять дивергенцию.
образует скалярное поле, от которого нельзя взять дивергенцию.
Всего осмысленных операций второго порядка пять:
1. 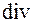
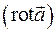 , 2.
, 2. 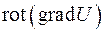 , 3.
, 3. 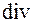
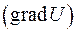 ,
,
4. 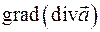 , 5.
, 5.  .
.
Рассмотрим эти комбинации.
1. 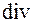
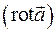
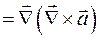 . Получили смешанное произведение трех векторов, два из которых равны между собой. В этом случае смешанное произведение равно нулю, т.е.
. Получили смешанное произведение трех векторов, два из которых равны между собой. В этом случае смешанное произведение равно нулю, т.е. 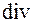
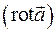 =0, а это означает, что поле ротора соленоидалъно.
=0, а это означает, что поле ротора соленоидалъно.
2. 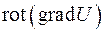
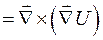 . Получили векторное произведение двух коллинеарных векторов
. Получили векторное произведение двух коллинеарных векторов 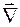 и
и 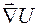 . Такое векторное произведение равно нулю, т.е.
. Такое векторное произведение равно нулю, т.е. 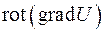
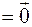 , значит, поле градиента потенциально.
, значит, поле градиента потенциально.
3. 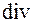
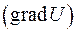
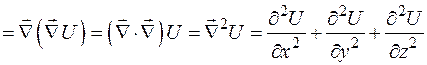 .
.
Оператор 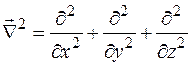 называется
называется  дифференциальным оператором Лапласа* или лапласианом и обозначается символом
дифференциальным оператором Лапласа* или лапласианом и обозначается символом 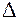 ("дельта"), т.е.
("дельта"), т.е.
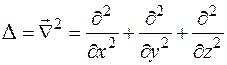 .
.
Дифференциальное уравнение в частных производных 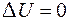 называется уравнением Лапласа. Оно имеет вид
называется уравнением Лапласа. Оно имеет вид
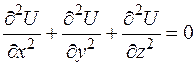 .
.
Можно рассматривать оператор Лапласа и соответственно уравнение Лапласа на плоскости, т.е.
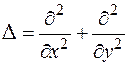 и
и 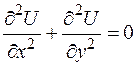 .
.
Функции, удовлетворяющие уравнению Лапласа, называются гармоническими (соответственно в пространстве или на плоскости).
Примерами гармонических функций в пространстве могут служить функции:  где
где  .
.
На плоскости примерами гармонических функций будут: 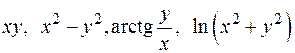 .
.
Дата публикования: 2014-11-19; Прочитано: 1514 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
