Решение задач. Задача 2.11.Показать, что скалярное поле является потенциалом векторного поля

Задача 2.11. Показать, что скалярное поле является потенциалом векторного поля .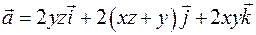

Решение. Покажем, что 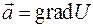, т.е., что выполняются равенства (2.20).

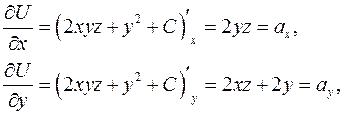
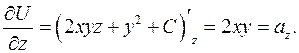
Задача 2.12. Показать, что векторное поле 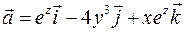потенциально и найти его потенциал.

Решение. Для доказательства потенциальности поля вычислим и воспользуемся формулой (2.21).

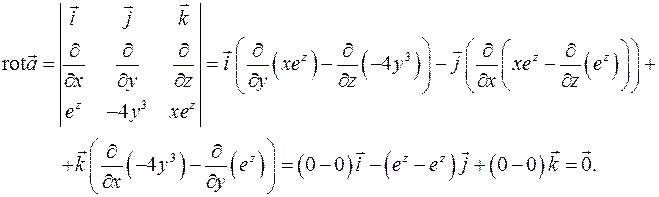Значит, поле потенциально.

Для нахождения потенциала воспользуемся формулой (2.23), а в качестве точки 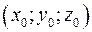возьмем точку .

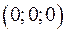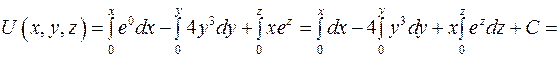
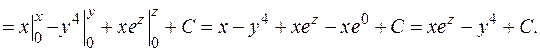
Задача 2.13. Проверить, будет ли векторное поле 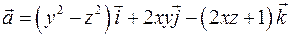соленоидальным.

Решение. Проверим, выполняется ли равенство (2.25).

Значит, поле соленоидально.

Задача 2.14. Проверить, будет ли векторное поле 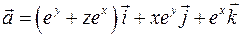гармоническим?

Решение. Векторное поле является гармоническим, если оно одновременно соленоидально и потенциально. Вычислим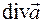

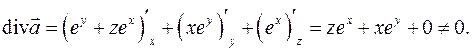
Значит, поле не является соленоидальным, и, следовательно, не является гармоническим.

Вопросы для самопроверки по теме 2.3

1. Дайте определение потенциального и соленоидального векторных полей.

2. Сформулируйте признаки потенциальности и соленоидальности векторных полей.

3. Перечислите свойства потенциальных векторных полей.

4. Перечислите свойства соленоидальных векторных полей.

5. Какое поле называется гармоническим?