Задание 3.3

3.3.0. Среди всех прямоугольников, имеющих данную площадь S, найти прямоугольник с наименьшим периметром.

3.3.1. Среди всех прямоугольников, имеющих данную площадь S, найти прямоугольник с наименьшей диагональю.

3.3.2. Найти наибольшую площадь прямоугольника, вписанного в круг радиуса R.

3.3.3. Найти на гиперболе 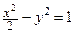точку, ближайшую к точке .

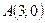3.3.4. Найти на параболе 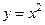точку, ближайшую к точке .

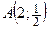3.3.5. Найти угловой коэффициент прямой, проходящей через точку 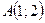и отсекающей от первого координатного угла треугольник наименьшей площади.

3.3.6. Найти длину боковой стороны трапеции, имеющей наименьший периметр среди всех равнобедренных трапеций с заданной площадью S и углом 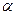между боковой стороной и нижним основанием.

3.3.7. Через точку 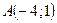провести прямую с положительным угловым коэффициентом такую, чтобы площадь треугольника, образованного ею с осями координат, была наименьшей.

3.3.8. Найти радиус основания и высоту прямого кругового цилиндра наибольшего объема, который можно вписать в шар радиуса R.

3.3.9. Найти стороны прямоугольника наибольшей площади, вписанного в эллипс 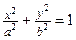так, что стороны прямоугольника параллельны осям эллипса.

Задание 3.4. Исследовать методами дифференциального исчисления функцию 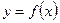и, используя результаты исследования, построить ее график.

3.4.0.	а)	б)
3.4.1.	а)	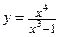б)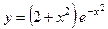
3.4.2.	а)	б)
3.4.3.	а)	б)
3.4.4.	а)	б)
3.4.5.	а)	б)
3.4.6.	а)	б)
3.4.7.	а)	б)
3.4.8.	а)	б)
3.4.9.	а)	б)