Вектор-функция скалярного аргумента. Уравнения , где , задают параметрически некот

Уравнения , где , задают параметрически некоторую кривую в пространстве Oxyz. Если 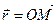– радиус-вектор точки , то конец переменного вектора

описывает кривую L. В векторной форме уравнение этой кривой можно записать в виде

;

– называется вектор-функцией (рис. 22).

Рис. 22.

Производная вектор-функции

представляет собой вектор, направленный по касательной к кривой L.

Уравнения касательной к кривой L в точке

:

Уравнение нормальной плоскости в точке M ₀:

Пример 3.9. Составить уравнения касательной и нормальной плоскости к кривой

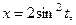
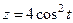
в точке .

Находим ,

.

При

.

Уравнения касательной: или в параметрической форме: где .

Эта прямая лежит в плоскости .

Уравнение нормальной плоскости:

или – плоскость, параллельная оси ординат.