Достаточное условие экстремума второго порядка

Если и , то функция имеет в точке экстремум, а именно, максимум, если , и минимум, если .

Для нахождения наибольшего (наименьшего) значения функции на отрезке нужно из значений функции на концах отрезка и в критических точках, принадлежащих интервалу , выбрать наибольшее (наименьшее).

Пример 3.5. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Из условия

находим критические точки: 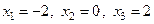. Точка не принадлежит отрезку .

Вычислим значения функции в критических точках внутри данного отрезка и на его границах.

, .

Наибольшее значение функции равно 16 и достигается в граничной точке , наименьшее значение равно –9 и достигается в критической точке: (точка минимума).

Пример 3.6. Среди всех равнобедренных треугольников, вписанных в данную окружность, найти треугольник с наибольшим периметром (рис. 19).

Рис. 19.

Решение. Пусть треугольник АВС вписан в окружность радиуса R, , как углы со взаимно перпендикулярными сторонами.

Из 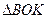имеем: 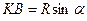, поэтому .

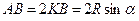Из находим:

.

Тогда .

Периметр треугольника ABC равен

и является функцией угла , .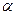

Вычислим производную от :

.

Из условия находим единственную критическую точку , принадлежащую интервалу .

При производная положительна, а при производная 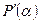отрицательна, следовательно, при функция достигает максимума.

– наибольшее значение на интервале . , значит, и , поэтому 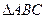– равносторонний.