 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Достаточное условие возрастания (убывания) функции на промежутке
|
|
Возрастание и убывание функции. Задачи на экстремум
Функция  называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале  , если для любых точек
, если для любых точек 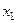 и
и  из указанного интервала, удовлетворяющих неравенству
из указанного интервала, удовлетворяющих неравенству 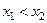 , выполняется неравенство:
, выполняется неравенство:
 для возрастающей функции и
для возрастающей функции и
 для убывающей функции.
для убывающей функции.
Достаточное условие возрастания (убывания) функции на промежутке
Если функция  дифференцируема на интервале
дифференцируема на интервале 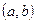 и
и  для
для  , то функция возрастает (убывает) на интервале
, то функция возрастает (убывает) на интервале 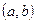 ,
,
Функция  имеет максимум (минимум) в точке
имеет максимум (минимум) в точке  , если существует такая окрестность точки
, если существует такая окрестность точки  , что для всех точек из этой окрестности, отличных от
, что для всех точек из этой окрестности, отличных от  , выполняется неравенство
, выполняется неравенство
 .
.
Точки максимума и точки минимума функции называются точками экстремума.
Дата публикования: 2014-11-19; Прочитано: 1470 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
