Асимптоты

Прямая называется асимптотой кривой 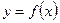, если расстояние точки кривой от этой прямой стремится к нулю при неограниченном удалении указанной точки по кривой от начала координат.

Различаются вертикальные и наклонные асимптоты.

Для отыскания вертикальных асимптот нужно найти такие значения 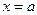, при приближении к которым функция 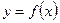неограниченно возрастает. Тогда прямая 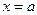будет вертикальной асимптотой.

Уравнение наклонной асимптоты имеет вид:

,

где k и b вычисляются по формулам:

, .

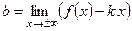В общем случае пределы 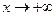при и при 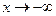различаются, и в таких случаях говорят о левой и правой наклонных асимптотах. Однако часто оказывается, что они совпадают, как в рассмотренных ниже примерах.

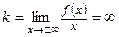Если или 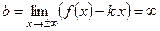, то наклонных асимптот нет.

Если 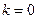, то прямая 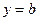– частный случай наклонной асимптоты – горизонтальная асимптота.

При построении графика функции 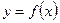нужно выяснить его характерные особенности.

Для этого необходимо

1) Найти область определения функции;

2) Исследовать функцию на четность и нечетность;

3) Найти точки пересечения графика функции с осями координат;

4) Исследовать функцию на непрерывность, найти точки разрыва (если они существуют) и установить характер разрывов, найти асимптоты кривой ;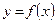

5) Найти интервалы возрастания и убывания функции и ее экстремумы;

6) Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.

Пример 3.7. Построить график функции

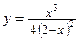
Решение.

1) Область определения функции – вся числовая ось Ох, кроме точки .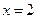

2) Функция не является ни четной, ни нечетной.

3) График функции пересекает обе координатные оси в точке (0;0).

Функция положительна при 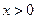, отрицательна при .

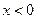4) Точка разрыва: 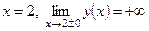, значит, – вертикальная асимптота.

Найдем наклонную асимптоту:

.

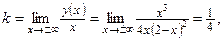
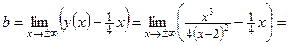
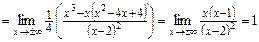Таким образом, уравнением наклонной асимптоты будет

.

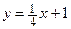5) Найдем экстремумы функции и интервалы возрастания и убывания, для чего вычислим производную

.

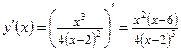Из условия 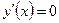, то есть 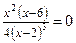, находим стационарные точки: 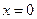, 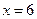. К ним добавляем точку , в которой 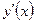не определена.

Таким образом, 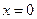, 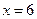; – критические точки.

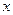
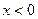
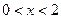
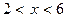
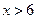
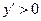
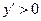
				не сущ.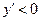
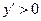
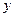
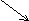
						min

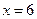– точка экстремума (минимум), .

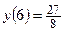На интервалах 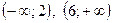функция возрастает, на интервале 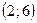– убывает.

6) Найдем интервалы выпуклости и вогнутости функции и точки перегиба, для чего вычислим вторую производную:

.

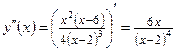Из условия 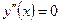, то есть 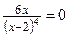, находим точку 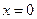. К ней добавляем точку , в которой 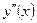не определена.

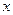
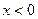
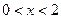
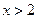
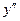
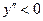
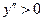
				не сущ.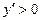
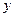
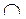
		т. перегиба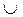

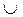
Таким образом, 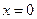– точка перегиба.

.

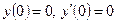При 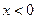график функции выпуклый и при 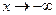приближается к асимптоте снизу.

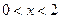При и при 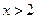– график функции вогнутый, и при 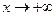он приближается к асимптоте сверху (рис. 20).

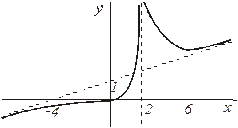
Рис. 20.

Пример 3.8. Построить график функции .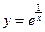

Решение.

1) Область определения функции – вся числовая ось Ох, кроме точки .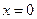

2) Функция не является ни четной, ни нечетной.

3) График функции расположен выше оси абсцисс в области ее определения, так как .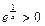

4) Точка разрыва: .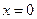

, .

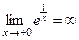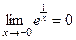Значит, 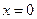является вертикальной асимптотой при .

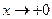Найдем наклонную асимптоту:

,

.

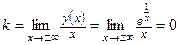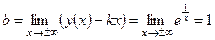Значит, 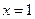– горизонтальная асимптота.

5) Найдем экстремумы функции и интервалы возрастания и убывания, для чего вычислим производную

.

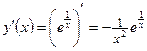Производная отрицательна при всех х 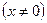, следовательно, функция убывает при всех х .

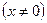6) Найдем интервалы выпуклости и вогнутости функции и точки перегиба, для чего вычислим вторую производную:

.

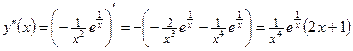Из условия 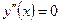находим .

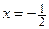К полученному значению 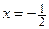добавляем точку 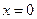, в которой 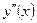не определена.

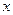
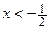
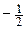
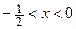
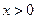
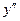
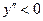
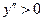
				не сущ.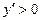
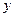
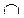
		т. перегиба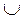

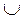
Таким образом, 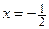– точка перегиба.

.

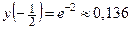При 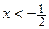график функции выпуклый и при 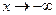приближается к асимптоте 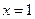снизу.

При график функции вогнутый. При 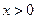график функции вогнутый и при 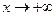приближается к асимптоте 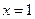сверху (рис. 21).

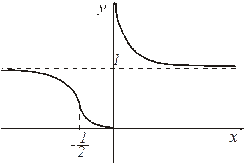
Рис. 21.