Сила тяги электромагнитов

а) Энергетический баланс электромагнита постоянно­го тока. Рассмотрим процесс возникновения магнитного поля в простейшем клапанном электромагните (рис. 4.1,а). После включения цепи напряжение источ­ника уравновешивается активным падением напряжения и э. д. с. самоиндукции

. (4.1)

Умножив обе части уравнения на idt, получим:

. (4.2)

Произведя интегрирование, получим:

, (4.3)

где потокосцепление к моменту времени

Левая часть равенства представляет энергию, кото­рая затрачена источником тока. Первый член правой части есть потери энергии в активном сопротивлении цепи, второй—энергия, затраченная на создание магнит­ного поля. До тех пор, пока сила, развиваемая элек­тромагнитом, меньше силы пружины, якорь электромаг­нита неподвижен, и потокосцепление нарастало при неизменном значении рабочего зазора . Зависимость при этом зазоре представлена кривой 1 рис..

Допустим, что при достижении значения потокосцепления сила электромагнита стала больше силы пру­жины и якорь переместился в положение, при котором рабочий зазор стал равен . Так как при меньшем за­зоре проводимость рабочего зазора возрастает, потокосцепление увеличится до значения . Величина тока при этом увеличится до значения 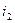. Если изобразить зависимость 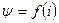при зазоре то получим кривую 2 рис.4.1 б. До начала трогания якоря энергия магнитного поля, запасенная в цепи, равна:

, (4.4)

где масштаб по оси тока, А/мм; масштаб по оси потокосцепления , -площадь криволинейного треугольника Оаb, .

При движении якоря потокосцепление изменится от до . Энергия магнитного поля приэтом возросла на величину.А₂, равную:

, (4.5)

где 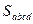площадь криволинейной трапеции.

При переходе от зазора к зазору якорь элек­тромагнита совершил механическую работу А₃.

Энергия, накопленная в магнитом поле, к концу хода равна А₄:

. (4.6)

На основании закона сохранения энергии можно на­писать:

. (4.7)

Механическая работа, совершенная якорем электро­магнита, определяется из

. (4.8)

Согласно рис. эта энергия равна:

. (4.9)

б) Расчет силы тяги электромагнита постоянного то­ка. Средняя сила на ходе якоря от до равна:

, (4.10

Рис.4.1.К определению силы тяги электромагнита

где перемещение якоря, а уменьшение зазора.

Следует учитывать, что (рис. 4.1, а). Тогда .

Для расчета силы, развиваемой электромагнитом, необходимо определить механическую работу А₃, совер­шаемую электромагнитом при небольшом перемещении якоря, после чего разделить эту работу на изменение зазора, что в пределе дает:

. (4.11)

Сила действует в сторону уменьшения зазора.

Очевидно, что для каждого элементарного переме­щения якоря можно определить свое А₃ и найти сред­нюю силу, развиваемую на данном участке хода якоря.

Зависимость тяговой силы электромагнита от вели­чины рабочего зазора при неизменном значении тока в его обмотке называется статической характеристикой электромагнита. Величина силы может быть найдена с помощью рис. 4.2:

(4.12)

Рис. 4.2. К определению силы тяги

Эта сила развивается электромагнитом при среднем зазоре

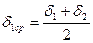. (4.13)

Аналогично определяется сила

. (4.14)

которая развивается при среднем зазоре

. (4.15)

На готовом электромагните статическая характеристика может быть легко снята. Для этого в воздушный зазор электромагнита ставится немаг­нитная прокладка, после чего к электромагниту подводится напряжение. С помощью динамоме­тра постепенно увеличивается противодействующая сила до тех пор, пока якорь не оторвется от сердечника. Эта сила в момент отрыва будет равна статическо­му усилию при зазоре, равном толщине прокладки. После этого меняют толщину прокладки и опыт повторяют при новом значении зазора.

Величина силы, развиваемой электромагнитом, мо­жет быть рассчитана с помощью формулы Максвелла. Если поле в рабочем зазоре равномерно и по­люсы ненасыщены, то формула Максвелла для силы в одном зазоре имеет вид

. (4.16)

в) Аналитический расчет силы для ненасыщенных электромагнитов. Исходя из закона сохранения энергии, можно показать, что энергия, полученная магнитным полем при элементарном перемещении якоря, равна механической работе, произведенной якорем, и измене­нию запаса электромагнитной энергии:

, (4.17)

где - элементарная энергия, полученная полем при перемещении якоря; элементарная работа, произведенная якорем; приращение магнитной энергии.

Из уравнения легко получить:

. (4.18)

Учитывая, что (для линейной магнитной цепи), получаем:

. (4.19)

Для статической тяговой характеристики 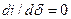, так как ток в цепи не меняется. Тогда

. (4.20)

Для клапанного электромагнита потокосцепление зависит от рабочего потока и потока рассеяния:

. (4.21)

Поскольку цепь линейна (пренебрегаем насыщением стали),то потокосцепление обусловленное рабочим потоком , равно:

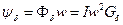. (4.22)

Потокосцепление , обусловленное потоком рассеяния, в свою очередь равно:

. (4.23)

Подставив 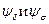, получим:

. (4.24)

Поскольку проводимость рассеяния от зазора не за­висит, то сила, развиваемая электромагни­том, будет равна:

. (4.25)

Если известна аналитическая зависимость , то находится дифференцированием. В уравнение (4.25) подставляется интересующего нас значения зазора . Если G₆ определяется в результате графического построения поля, то вначале производится расчет G₆ для ряда положений якоря, после чего графически строится зависимость и производится графическое дифференцирование.

При достаточно малом зазоре для системы рис. 3.1

. (4.26)

Тогда величина силы F равна:

. (4.27)

Согласно выражению сила, развиваемая электромагни­том, пропорциональна квадрату н. с. катушки, площади полюса и обратно пропорциональна квадрату величины зазора. Зависимость при неизменной н. с. катушки представлена на рис. 4.3 (кривая 1). По мере уменьшения величина силы резко возрастает, причем при = 0 сила принимает бесконечное значение. В дей­ствительности при = 0 величина потока в системе опре­деляется магнитным сопро­тивлением цепи, которое резко возрастает по мере насыщения материала магнитопровода, и сила имеет конечное значение. Кривая 2 на рис.4.3 изображает зависимость , снятую эксперимен­тально. Сравнение этих кри­вых показывает, что при больших зазорах, когда поток в системе мал и паде­нием магнитного потенциала в сердечнике можно пре­небречь, расчетная и экспериментальная кривые почти полностью совпадают. При малых зазорах сила, разви­ваемая электромагнитом, имеет конечное значение.

Рис. 4.3. Тяговая характеристика

Многочисленные исследования пока­зали, что для расчета силы в насыщенных электромаг­нитах можно пользоваться формулой (4.25), но только вместо берется падение магнитного потенциала в рабочем зазоре:

. (4.28)

Величину 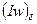находят в результате расчета магнитных цепей.

Поскольку формула Максвелла учитывает реальную индукцию между полюсами, то она также мо­жет быть использована при условии, что поле в зазоре равномерно и вектор индукции перпендикулярен к по­верхности полюса.

г) Сила тяги электромагнита переменного тока. Рас­смотрим задачу применительно к клапанному электро­магниту с двумя рабочими зазорами, сделав следующие допущения: магнитное сопротивление стали, активное сопротивление обмотки и потери в стали рав­ны нулю; напряжение, ток и поток меняются по синусо­идальному закону.

В этом случае поток, а следовательно, потокосцепление не зависят от величины зазора .

Тогда мгновенное значение силы будет равно:

. (4.29)

Подставив, получим:

. (4.30)

Поскольку и 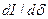при данном зазоре не зависят от времени, можно записать:

. (4.31)

Производная может быть найдена графическим дифференцированием зависимости , которая получается из расчета магнитной цепи. Величина определяется приложенным напряжением.

Мгновенное значение силы при наличии двух рабо­чих зазоров может быть найдено по формуле Максвел­ла (4.16). Для амплитуды силы получим:

.

Поскольку при изменении зазора амплитуда потока и индукции не изменяются, амплитуда силы от зазора не зависит. Однако если учесть активное сопротивление обмотки, то, как было показано, с ростом зазора поток в системе уменьшается, что приводит к уменьше­нию амплитуды силы.

Рассмотрим теперь изменение силы во времени. Со­гласно (4.31) сила меняется во времени по следующему закону:

. (4.32)

Мгновенное значение силы пульсирует с двойной часто­той по отношению к частоте тока. Среднее значение силы равно половине амплитудного значения:

. (4.33)

Для притяжения якоря необходимо, чтобы среднее зна­чение силы было больше противодействующего усилия.

Изменение силы во времени отрицательно сказывает­ся на работе электромагнита. В определенные моменты времени сила противодействующей пружины становится больше силы электромагнита, при этом происходит от­рыв якоря от сердечника. По мере нарастания силы электромагнита снова происходит притяжение якоря. В результате якорь электромагнита будет непрерывно вибрировать, создавая шум и ненормальные условия ра­боты механизма или контактов. В связи с этим прини­маются меры для устранения вибрации.

В однофазных электромагнитах наибольшее распро­странение получило использование короткозамкнутого витка. Эскиз полюса такого электромагнита представ­лен на рис.4.4. Наконечник полюса расщеплен, и на большую его часть насажен короткозамкнутый виток, выполненный из меди или алюминия. Для получения бо­лее ясной картины примем, что сопротивление стали рав­но нулю и существует только один рабочий зазор.

Благодаря наличию короткозамкнутого витка поток отстает по фазе относительно на угол . Каждый из потоков под своей частью по­люса создает свою силу и .

В верхней части полюса развивается сила , равная:

. (4.34)

В нижней части полюса развивается сила , равная:

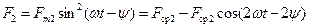. (4.35)

Результирующая сила, действующая на якорь, равна сумме сил и .

Если изобразить соответствующими векторами, то амплитуда пе­ременной составляющей может быть найдена из вектор­ной диаграммы

. (4.36)

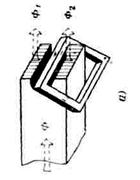
Рис. 4.4. Полюсный наконечник с к.з. витком

Обычно электромагнит проектируется таким образом, чтобы минимальная сила F_MI, развиваемая электромаг­нитом, была больше противодействующей силы:

. (4.37)

Очевидно, что чем меньше , тем меньше будет пульсация силы . Из уравнения следует, 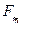что равно нулю при и . При таком соотношении величин в момент перехода через нуль силы сила достигает максимального значения. В любой точке сумма + равна постоянной величине. Поскольку короткозамкнутый виток уменьшает поток под нижней частью полюса, то с целью выравнивания и 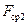этот виток охватывает большую часть полюса (обычно ²/₃).

Угол сдвига фаз зависит от магнитного сопротив­ления зазора R _Ь2 и параметров короткозамкнутого витка:

. (4.38)

Откуда следует, что чем больше рабочий зазор, а сле­довательно, и тем меньше будет угол . В связи с этим короткозамкнутый виток оказывает положительный эффект только при малых зазорах. При больших зазорах 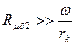и угол .Следовательно, никакого сдвига фаз между потоком Ф1 и Ф2 не будет. Индуктивное сопротивление витка также уменьшает угол поскольку при этом уменьшается . Обычно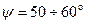

При наличии трехфазного источника питания для уменьшения вибрации можно использовать естественный сдвиг потоков в этой системе.

Если принять, что в магнитном отношении все три фазы магнита симметричны и насыщение отсутствует, то величина силы, развиваемой под каждым полюсом, будет равна:

(4.39)

Результирующая сила, действующая на якорь, равна сумме этих сил:

. (4.40)

Таким образом, в трехфазном электромагните резуль­тирующая сила, действующая на якорь, во времени не меняется. Однако и в этом электромагните вибрация якоря полностью не устраняется. При прохождении по­тока в каждой фазе через нуль сила, развиваемая этой фазой, также равна нулю. В результате точка приложе­ния электромагнитной силы перемещается. Поскольку точка приложения противодействующей силы неизменна, то возникает перекатывание якоря, т.е. вибрация.