Нагрев электроаппаратов. Нормы нагрева, термическая устойчивость

ЭЛЕКТРОДИНАМИЧЕСКИЕ УСИЛИЯ В ЭЛЕМЕНТАХ АППАРАТОВ

При коротком замыкании в сети через токоведущую часть ап­парата могут протекать токи, в десятки раз превышающие номи­нальные. Эти токи, взаимодействуя с магнитным полем, создают электродинамические усилия (э. д. у.), которые стремятся деформировать проводники и изоляторы, на которых они крепятся. В некоторых случаях величина э. д. у. может достигать десятков тонн, при этом возможно даже разрушение аппарата.

Для определения э. д. у. используются два метода.

В первом методе сила рассматривается как резуль­тат взаимодействия проводника с током и магнитным полем. Если элементарный проводник dl с током i находится в магнитном поле с индукцией создаваемой 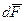другими проводниками, то сила действующая на этот элемент, равна

, (6.1)

где угол между векторами элемента dl и индукции В.

За направление dl принимается направление тока в этом элементе.

Направление индукции, создаваемой проводником, легко найти с помощью правила буравчика. Если винт буравчика движется вдоль тока в проводнике, то направление вращения рукоятки совпа­дает с направлением магнитной силовой линии, т. е. с вектором индукции.

Направление силы можно определить по правилу левой руки. Для этого левую руку располагают так, чтобы вектор индукции пронизывал ладонь, а направление тока в проводнике совпадало с четырьмя вытянутыми пальцами. Тогда направление силы будет указывать большой палец (рис.6.1).

Правило буравчика можно использовать и для определения направления результирующего вектора следовательно, и направления силы.

Если рукоятку штопора вращать от вектора к вектору по кратчайшему расстоянию, то направление движения винта што­пора совпадает с направлением силы, действующей на элемент с током .

Рис.6.1. Правило левой руки

Для определения полной силы, действующей на проводник длиной l, необходимо просуммировать силы, действующие на все его элементы:

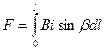. (6.2)

В случае любого расположения про­водников в одной плоскости 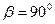уравнение упрощается:

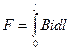. (6.3)

Описанный метод рекомендуется при­менять тогда, когда можно аналитически найти индукцию в любой точке провод­ника, для которого необходимо опреде­лить силу.

Второй метод определения э. д. у. основан на использовании энергетического баланса системы проводников с током. Если пренебречь электростатической энергией системы и при­нять, что при деформации токоведущих контуров или их переме­щении под действием э. д. у. величина тока во всех контурах оста­ется неизменной, то силу можно найти по уравнению

, (6.4)

где A- электромагнитная энергия;

x- возможное перемещение в направлении действия силы F.

Таким образом, сила равна частной производной от электро­магнитной энергии данной системы по координате, в направлении которой действует сила.

Электромагнитная энергия системы обусловлена как энергией магнитного поля каждого изолированного контура, так и энер­гией, определяемой магнитной связью между контурами.

Для системы трех взаимосвязанных контуров электромагнит­ная энергия

, (6.5)

здесь индуктивности контуров;

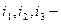токи в контурах;

взаимоиндуктивности между контурами.

Первые три члена уравнения определяют энергию независимых контуров, вторые три члена характеризуют энергию, обусловлен­ную магнитной связью.

Уравнение дает возможность рассчитать как силы, дей­ствующие в изолированном контуре, так и силу взаимодействия этого контура со всеми остальными.

При коротком замыкании величина тока в цепи не зависит от незначительных деформаций токоведущих контуров или от изме­нения расстояния между ними, возникающих под действием э. д. у. Поэтому при нахождении сил с помощью уравнения можно считать, что величина тока не меняется, а сила возникает в резуль­тате изменения индуктивности или взаимоиндуктивности.

Для определения сил внутри одного контура пользуются урав­нением

, (6.6)

где х — координата, в направлении которой действует сила F.

При расчете силы, действующей между контурами, считаем, что энергия меняется только в результате возможного изменения взаимного расположения контуров. При этом энергия, обусловленная собствен­ной индуктивностью, считается неиз­менной:

. (6.7)

Энергетическим методом очень удобно пользоваться тогда, когда известна ана­литическая зависимость индуктивности или взаимоиндуктивности от геометри­ческих параметров.

Этот метод позволяет легко найти на­правление э. д. у. Из уравнения (6.4) следует, что положительному направлению силы F соответствует возрастание энергии системы , т.е. деформация контура или его перемещение происходит под действием силы таким образом, чтобы электромагнитная энергия системы воз­растала.

Электромагнитная энергия одного контура

, (6.8)

где потокосцепление;

магнитный поток;

число витков в контуре.

Сила, действующая в контуре, будет направлена таким обра­зом, чтобы индуктивность, потокосцепление и поток при деформа­ции контура под действием этой силы возрастали.

Возьмем для примера круговой виток рис.6.2.

Рис. 6.2. Силы в витке, обтекаемом током

Если , то индуктивность витка достаточно точно выражается уравнением

При протекании тока возникает сила, стремящаяся увеличить радиус витка, поскольку с ростом R растет индуктивность L, а следовательно, увеличивается и электромагнитная энергия систе­мы:

. (6.9)

С ростом радиуса возрастает потокосцепление данного контура при условии, что ток в цепи не меняется.

ЭЛЕКТРОДИНАМИЧЕСКИЕ СИЛЫ, ВОЗНИКАЮЩИЕ ПРИ ИЗМЕНЕНИИ СЕЧЕНИЯ ПРОВОДНИКА

При протекании тока по цилиндрическому проводнику на от­дельные нити тока действуют э. д. у., стремящиеся переместить эту нить к центру проводника. Поскольку все линии тока верти­кальны, а индукция в любой точке проводника направлена по ка­сательной, то сила, действующая на элементарные нити, направ­лена по радиусу и не имеет осевой составляющей.

При изменении сечения проводника линии тока искривляются и, кроме поперечной сжимающей силы, возникает продольная, стре­мящаяся разорвать место перехода вдоль оси проводника. Как видно из рис.6.3, сила, возникающая в месте перехода, направ­лена в сторону большего сечения.

Рис.6.3. Электродинамические силы, действующие в месте изменения

поперечного сечения проводника

Формула для расчета этих сил имеет вид:

(6.10)

Следует отметить, что эта формула справедлива для любого сим­метричного перехода от сечения с радиусом г_к к сечению с радиу­сом г_и. Так, в случае многократного конуса

, (6.11)

где радиус конечного сечения;

радиус начального сечения.

Плавный переход от одного сечения к другому можно рассматри­вать как переход, образованный большим числом конусных перехо­дов. Таким образом, электродинамическая сила, возникающая при изменении сечения, зависит только от отношения конечного и началь­ного радиусов и не зависит от формы перехода. Этот вывод справед­лив для равномерного распределения тока по сечению проводника.

Известно, что в электрическом контакте при переходе тока из одного контакта в другой происходит искривление линий тока, аналогичное показанному на рис. 6.3. Для одноточечного контакта касание контактов происходит по площадке смятия. Если положить, что эта площадка находится в цент­ре цилиндрических проводников, то сила, действующая на каждый кон­такт, может быть рассчитана по формуле

, (6.12)

где радиус цилиндрического контакта;

радиус круглой площадки касания.

При номинальном токе эта отбрасывающая сила ничтожна. При коротком замыкании в одноточечном контакте отбрасывающая сила может достигать сотен ньютонов. Для того чтобы контакт был динамически устойчив, сила нажа­тия должна быть больше силы отброса.

В реальных контактах, кроме силы отброса, возникающей из-за изменения сечения проводника, появляется дополнительное э. д. у. за счет взаимодействий, создаваемых токоведущим контуром.

СИЛЫ ВТЯГИВАНИЯ ДУГИ (ПРОВОДНИКА) В СТАЛЬНУЮ РЕШЕТКУ

В дугогасительных камерах аппаратов высокого и низкого напряжений применяется решетка из набора ферромагнитных пла­стин с пазами.

Электрическая дуга, возникающая между контактами аппа­рата, является своеобразным проводником тока. Взаимодействие этого проводника с решеткой создает электромагнитную силу, двигающую ду­гу. Наиболее широко распространены решетки из стальных пластин с клино­видными пазами.

Рассмотрим силу, действующую на проводник (дугу), симметрично расположенный в пазу прямоугольного сечения (рис.6.3).

При расчете примем сле­дующие упрощения: магнитное сопро­тивление стали равно нулю; потоком рассеяния, выходящим с торца решетки пренебрегаем; ток течет по геометрической ОСИ проводника.

В данном случае для расчета силы удобно воспользоваться энергетическим методом. Сила, действующая на проводник, в данном случае бу­дет равна

. (6.13)

Индуктивность системы L можно выразить через поток

. (6.14)

Поскольку , тогда

. (6.15)

Поток, связанный с проводником, равен

, (6.16)

где – ;

l – активная длина решетки;

x– расстояние от проводника до начала паза;

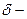ширина паза.

Подставляя, получим

(6.17)

При сделанных допущениях сила, действующая на проводник, не зависит от положения проводника в пазу.

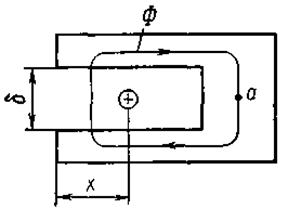Рис.6.4.К расчету сил, действующих на проводник

расположенный в прямоугольном пазу ферромагнитного тела

В дугогасительных устройствах низкого напряжения дуга, втягиваясь в решетку, пересекает ее и останавливается в точке а, в которой сила, действующая на дугу, должна быть равна нулю.

Это может быть при ,т. е. дуга остановится в точке, где поток достигает максимального значения. Поскольку то эта точка также соответствует максимуму электромагнитной энергии. По мере движения дуги вверх проводимость нижней части магнитной цепи растет линейно с х. В точке а об­щая проводимость цепи будет максимальна. Если дуга пройдет выше нее, то поток начнет снова убывать и возникнет сила, стремящаяся вер­нуть дугу опять в точку а.

В реальном аппарате картина зна­чительно усложняется, поскольку по мере продвижения дуги вверх растет поток в цепи и наступает насыщение верхней части пластин решетки. Если опытным путем, с помощью измерительной катушки получить зависи­мость Ф _x = f(х), заменив дугу про­водником, то величина силы, действующей на дугу, может быть достаточно точно рассчитана с учетом сопротивления стали по следующей формуле:

, (6.18)

где находится графическим дифференцированием опытной кривой . Для клиновидной щели (рис.6.5) сила, действующая на дугу, может быть также рассчитана по уравнению (6.16), если принять те же допущения, что и для прямоугольной щели:

(6.20)

здесь 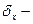воздушный зазор на расстоянии х от начала решетки

Рис. 6.5. К расчету сил, действующих на проводник,

расположенный в суживающемся пазу ферромагнитного тела

Подставив в уравнение для силы, получим

. (6.21)

В отличие от предыдущего случая по мере роста х₁ величина силы увеличивается и достигает бесконечной величины при х₁ =h. В действительности, по мере уменьшения 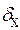будет возрастать па­дение магнитного потенциала в стали. В этом случае мы не имеем права пользоваться уравнением. При х₁ =h вся намагни­чивающая сила проводника становится равной падению магнит­ного потенциала в стали. Уравнением можно пользоваться только тогда, когда падение магнитного потенциала в стали не­велико (не более 10% от общей намагничивающей силы).

Сила, действующая на дугу, может значительно искажаться ее формой. После расхождения контактов дуга имеет форму не прямолинейного проводника, а скорее форму части окружности. Это при­водит к тому, что сначала в решетку входит средняя часть дуги, а потом ее крайние части. Кроме того, дуга может не располагаться точно по оси паза, что также затрудняет расчет. Формулы могут быть использованы только для ориентировочных расчетов. Для более точных расчетов рекомендуется опытным пу­тем снимать зависимость и пользоваться графическим дифференцированием.

Аналогичные силы возникают между проводником и ферромагнитным телом, поскольку при приближении проводника к телу обязательно возрастает поток и, следовательно, увеличивается электромагнитная энергия системы.