Магнитные цепи с постоянными магнитами

а) Общие сведения. Для создания постоянного маг­нитного поля в целом ряде электрических аппаратов ис­пользуются постоянные магниты, которые изготавлива­ются из магнитно-твер­дых материалов, имею­щих широкую петлю ги­стерезиса (рис.5.6).

Работа постоянного магнита происходит на участке от H= 0 до H = — Н_с. Эта часть петли называется кривой размагничивания.

Рассмотрим основные соотношения в постоян­ном магните, имеющем форму тороида с одним малым зазором б (рис.5.6). Благодаря форме тороида и небольшому зазору потоками рассеяния в таком магните можно пренебречь. Если зазор мал, то магнитное поле в нем можно счи­тать однородным.

Рис.5.6. Кривая размагничивания постоянного магнита

Если пренебречь выпучиванием, то индукции в зазоре В_& и внутри магнита В одинаковы.

На основании закона полного тока при интегрирова­нии по замкнутому контуру 1231 рис. получим:

. (5.28)

Рис.5.7. Постоян­ный магнит, имеющий форму тороида

Таким образом, напряженность поля в зазоре направ­лена встречно напряженности в теле магнита. Для элек­тромагнита постоянного тока, имеющего аналогичную форму магнитной цепи, без учета насыщения можно написать: .

Сравнивая мож­но видеть, что в случае с постоян­ным магнитом н. с, создающей поток в рабочем зазоре, является про­изведение напряженности в теле магнита на его длину с обратным знаком — Hl.

Воспользовавшись тем, что

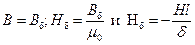, (5.29)

получим:

, (5.30)

или

, (5.31)

где S -площадь полюса; - проводимость воздушного зазора.

Уравнение есть уравнение прямой, проходя­щей через начало координат во втором квадранте под углом а к оси Н. С учетом масштаба индукции т_в и на­пряженности т_н угол а определяется равенством

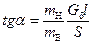. (5.32)

Так как индукция и напряженность магнитного поля в теле постоянного магнита связаны кривой размагничи­вания, то пересечение указанной прямой с кривой раз­магничивания (точка А на рис.5.6) и определяет со­стояние сердечника при заданном зазоре.

При замкнутой цепи и

(5.33)

С ростом б проводимость рабочего зазора и tga уменьшаются, индукция в рабочем зазоре падает, а на­пряженность поля внутри магнита увеличивается.

Одной из важных характеристик постоянного магни­та является энергия магнитного поля в рабочем зазоре W_t. Учитывая, что поле в за­зоре однородно,

. (5.34)

Подставляя значение Н_ь получим:

, (5.35)

где V_M — объем тела магнита.

Таким образом, энергия в рабочем зазоре равна энер­гии внутри магнита.

Зависимость произведения В(—Н) в функции индук­ции показана на рис.5.6. Очевидно, что для точки С, в которой В(—Н) достигает максимального значения, энергия в воздушном зазоре также достигает наиболь­шей величины, и с точки зрения использования постоян­ного магнита эта точка является оптимальной. Можно показать, что точка С, соответствующая макси­муму произведения , есть точка пересечения с кривой размагничивания луча О К, проведенного через точку с координатами и .

Рассмотрим более подробно влияние зазора б на ве­личину индукции В (рис.5.6). Если намагничивание магнита производилось при зазоре б, то после снятия внешнего поля в теле магнита установится индукция, соответствующая точке А. Положение этой точки опреде­ляется зазором б.

Уменьшим зазор до значения 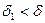, тогда

. (5.36)

При уменьшении зазора индукция в теле магнита воз­растает, однако процесс изменения индукции идет не по кривой размагничивания, а по ветви частной петли гистерезиса AMD. Индукция В ₁определяется точкой пересечения этой ветви с лучом, проведенным под углом к оси — Н (точка D).

Если мы снова увеличим за­зор до значения б, то индукция будет падать до значения В, при­чем зависимость В (Н) будет определяться ветвью DNA частной петли гистерезиса. Обычно частная петля гистерезиса AMDNA достаточно узка и ее заменяют прямой AD, которую на­зывают прямой возврата. Наклон к горизонтальной оси (+ Н) этой прямой называется коэффициентом возврата:

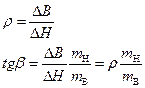. (5.37)

Характеристика размагничивания материала обычно не приводится полностью, а задаются только величины индукции насыщения B_s, остаточной индукции В_г, коэр­цитивной силы Н_с. Для расчета магнита необходимо знать всю кривую размагничивания, которая для боль­шинства магнитно-твердых материалов хорошо аппроксимируется формулой

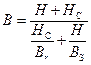. (5.38)

Кривая размагничивания, выражаемая (5.30), мо­жет быть легко построена графически, если известны B_s, В_r.

б) Определение потока в рабочем зазоре для задан­ной магнитной цепи. В реальной системе с постоянным магнитом поток в рабочем зазоре отличается от потока в нейтральном сечении (середине магнита) из-за наличия потоков рассеяния и выпучивания (рис.).

Поток в нейтральном сечении равен:

, (5.39)

где 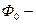поток в нейтральном сечении;

поток выпучивания у полюсов;

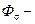поток рассеяния;

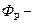рабочий поток.

Коэффициент рассеяния о определяется равенством

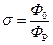. (5.40)

Если принять, что потоки 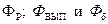создаются одной и той же разностью магнитных потенциалов, то

. (5.41)

Индукцию в нейтральном сечении найдем, определив :

,

и воспользовавшись кривой размагничивания рис.5.6. Индукция в рабочем зазоре равна:

, (5.42)

поскольку поток в рабочем зазоре в раз меньше, чем поток в нейтральном сечении.

Очень часто намагничивание системы происходит в несобранном состоянии, когда проводимость рабочего зазора уменьшена из-за отсутствия деталей из ферро­магнитного материала. В этом случае расчет ведется с ис­пользованием прямой возврата. Если потоки рассеяния значительны, то расчет реко­мендуется вести по участкам, так же как и в случае элек­тромагнита.

Потоки рассеяния в постоянных магнитах играют зна­чительно большую роль, чем в электромагнитах. Дело в том, что магнитная проницаемость магнитно-твердых материалов значительно ниже, чем у магнитно-мягких, из которых изготавливаются системы для электромагни­тов. Потоки рассеяния вызывают значительное падение магнитного потенциала вдоль постоянного магнита и уменьшают н. с, а следовательно, и поток в рабочем зазоре.

Коэффициент рассеяния выполненных систем ко­леблется в довольно широких пределах. Расчет ко­эффициента рассеяния и потоков рассеяния связан с большими трудностями. Поэтому при разработке новой конструкции величину коэффициента рассеяния реко­мендуется определить на специальной модели, в которой постоянный магнит заменен электромагнитом. Намагничивающая обмотка выбирается такой, чтобы по­лучить в рабочем зазоре необходимый поток.

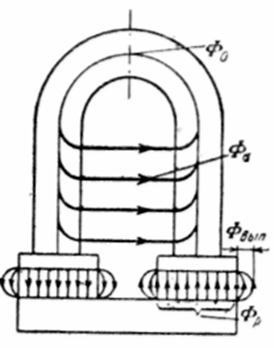
Рис.5.8. Магнитной цепи с постоянным магнитом и потоками рассеяния и выпучивания

в) Определение размеров магнита по требуемой ин­дукции в рабочем зазоре. Эта задача является еще более трудной, чем определение потока при известных разме­рах. При выборе размеров магнитной цепи обычно стремятся к тому, чтобы индукция В₀ и напряженность Н₀ в нейтральном сечении соответствовали максимальному значению произведения Н₀В₀. При этом объем магнита будет минимальным. Даются следую­щие рекомендации по выбору материалов. Если требу­ется при больших зазорах получить большое значение индукции, то наиболее подходящим материалом является магнико. Если при большом зазоре необходимо создать небольшие индукции, то можно рекомендовать альниси. При малых рабочих зазорах и большом значении индук­ции целесообразно применение альни.

Сечение магнита выбирается из следующих сообра­жений. Индукция в нейтральном сечении выбирается равной В₀. Тогда поток в нейтральном сечении

,

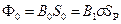откуда сечение магнита

.
Величины индукции в рабочем зазоре В_р и площадь полюса являются заданными величинами. Наиболее трудным является определение значения коэффициента рассеяния. Величина его зависит от конструкции и индукции в сердечнике. Если сечение магнита получилось большим, то применяют не­сколько магнитов, включенных параллельно. Длина маг­нита определяется из условия создания необходимой н.с. в рабочем зазоре при напряженности в теле магнита Н₀:

,

где б _р — величина рабочего зазора.

При больших рабочих зазорах рекомендуется соеди­нять несколько магнитов последовательно.

После выбора основных размеров и конструирования магнита проводится поверочный расчет по методике, опи­санной ранее.

г) Стабилизация характеристик магнита. В процессе работы магнита наблюдается уменьшение потока в ра­бочем зазоре системы — старение магнита. Различают структурное, механическое и магнитное старение.

Структурное старение наступает вследствие того, что после закалки материала в нем возникают внутренние напряжения, материал приобретает неоднородную струк­туру. В процессе работы материал становится более од­нородным, внутренние напряжения исчезают. При этом остаточная индукция В_т и коэрцитивная сила Н_с умень­шаются. Для борьбы со структурным старением мате­риал подвергается термообработке в виде отпуска. При этом внутренние напряжения в материале исчезают. Его характеристики становятся более стабильными. Алюминиево-никелевые сплавы (альни и др.) не требуют струк­турной стабилизации.

Механическое старение наступает при ударах и ви­брациях магнита. Для того чтобы сделать магнит нечув­ствительным к механическим воздействиям, его подвер­гают искусственному старению. Образцы магнита перед установкой в аппарат подвергаются таким ударам и ви­брации, которые имеют место в эксплуатации.

Магнитное старение — изменение свойств материала под действием внешних магнитных полей. Положитель­ное внешнее поле увеличивает индукцию по прямой воз врата, а отрицательное снижает ее по кривой размагни­чивания. Для того чтобы сделать магнит более стабиль­ным, его подвергают действию размагничивающего поля, после чего магнит работает на прямой возврата. Из-за меньшей крутизны прямой возврата влияние внешних полей уменьшается. При расчете магнитных систем с по­стоянными магнитами необходимо учитывать, что в про­цессе стабилизации магнитный поток уменьшается на 10-15%.