Общие сведения о магнитных цепях аппаратов

а) Магнитная цепь аппарата, основные законы. Электромагниты нашли в аппаратостроении широкое при­менение и как элемент привода аппаратов (контакторы, пускатели, реле, автоматы, выключатели) и как устройство, создающее силы в муфтах, тормозах и подъемных механиз­мах.

Конфигурация магнитной це­пи электромагнита зависит от на­значения аппарата и может быть самой разнообразной.

Основные соотношения для магнитной цепи мы рассмотрим на примере клапанной системы, изображенной на рис. 3.1. По­движная часть магнитной цепи называется якорем 1. Часть магнитной цепи, на которой си­дит намагничивающая катушка 2, называется сердечником 3. Вертикальные и параллельные части магнитопровода 3 и 4 ча­сто называют стержнями.

В клапанной системе якорь может иметь как поступательное движение так и вращательное.

Намагничивающая катушка создает намагничиваю­щую силу (н. с), под действием которой возбуждается магнитный поток. Этот поток замыкается как через за­зор б, так и между другими частями магнитной цепи, имеющими различные магнитные потенциалы.

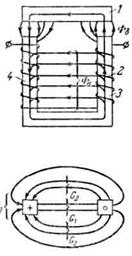Рис. 3.1. Магнитная цепь клапанной системы

Воздушный зазор б, меняющийся при перемещении якоря, называется рабочим зазором. Соответ­ственно поток, проходящий через рабочий зазор, назы­вается рабочим потоком и обозначается обычно Ф₅. Все остальные потоки в магнитной цепи называются потоками рассеяния Ф_в. Сила, развиваемая 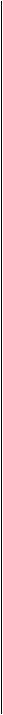якорем электромагнита, как правило, определяется по­током в рабочем зазоре Ф_ъ.

Задачей расчета магнитной цепи является либо определение н. с. катушки, необходимой для создания рабочего потока заданной величины (прямая задача), либо определение рабочего потока по известной н. с. катушки (обратная задача). Эти задачи могут быть решены с помощью двух законов Кирхгофа примени­тельно к магнитной цепи.

Согласно первому закону алгебраическая сумма по­токов в узле магнитной цепи равна нулю:

(3.1)

Второй закон Кирхгофа можно получить из известного закона полного тока

(3.2)

где Н — напряженность магнитного поля;

dl — элемент длины, по которому проходит магнитный поток;

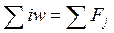— сумма н. с., действующих в контуре.

Помня, что , можно написать в виде

, (3.3)

где S — сечение магнитной цепи; µ— магнитная про­ницаемость.

Магнитная проницаемость µхарактеризует прово­димость магнитного материала цепи. Выражение d l/µS аналогично сопротивлению элемента электрической це­пи dl/x (где х — электрическая проводимость мате­риала проводника). Тогда можно представить в виде

, (3.4)

где dR — магнитное сопротивление участка дли­ной- dl.

Падение магнитного потенциала по замкнутому кон­туру равно сумме намагничивающих сил, действующих в этом контуре. Это и есть второй закон Кирхгофа маг­нитной цепи.

В системе единиц СИ размерность 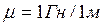, сле­довательно, магнитное сопротивление получает размер­ность µ=1/1 Гн — единица, деленная на генри.

В том случае, когда поток в отдельных частях маг­нитной цепи не меняется, интеграл можно за­менить конечной суммой

. (3.5)

Таким образом, сумма падений магнитного напря­жения по замкнутому контуру равна сумме намагничи­вающих сил, связанных с потоками, проходящими че­рез магнитную цепь.

По аналогии с электрической цепью магнитное со­противление участка конечной длины l можно предста­вить в виде

, (3.6)

где —магнитное сопротивление единицы длины магнитной цепи при сечении, также равном единице, м/гн.

Полная аналогия законов Кирхгофа электрической и магнитной цепей позволяет составить для последней электрическую схему замещения.

Для расчета по (3.5) необходимо иметь кривую (В), Если задана не кривая (В), а кривая намаг­ничивания материала В(Н), для расчета удобно ис­пользовать (3.2). Если на отдельных участках индук­ция постоянна, то интеграл в (3.2) можно заменить ко­нечной суммой

. (3.7)

По известной индукции в каждом участке с помощью кривой В(Н) находят напряженность Hj на участке, после чего с помощью (3.7) можно отыскать потребную н. с. катушки.

При расчете магнитной цепи часто более удобным является введение величины, обратной магнитному со­противлению — магнитной проводимости

. (3.8)

Уравнение (3.5) при этом принимает вид:

(3.9)

Для простейшей неразветвленной цепи

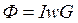. (3.10)

Магнитное сопротивление и проводимость ферромаг­нитных материалов являются сложной нелинейной функцией индукции. Зависимость относительной магнит­ной проницаемости , а следовательно, и магнит­ной проводимости от величины индукции для магнитномягкого материала пред­ставлена на рис.1.2. Макси­мальное значение (ми­нимальное магнитное сопро­тивление) имеет место при средних величинах индук­ции. В слабых и сильных полях магнитное сопротив­ление материала резко воз­растает. Изменение магнит­ного сопротивления от ве­личины индукции сильно затрудняет решение как прямой, так и обратной задачи.