 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница
|
|
Пусть функция 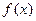 интегрируема на
интегрируема на  ,
,  ,
,  . Тогда функция
. Тогда функция
 называется интегралом с переменным верхним пределом. Перечислим основные его свойства.
называется интегралом с переменным верхним пределом. Перечислим основные его свойства.
1. Если 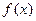 интегрируема на
интегрируема на  , то функция
, то функция  непрерывна для любого
непрерывна для любого  .
.
2. Если 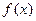 непрерывна в точке
непрерывна в точке  , то функция
, то функция  имеет производную в этой точке, и
имеет производную в этой точке, и  . Поэтому всякая непрерывная функция имеет первообразную.
. Поэтому всякая непрерывная функция имеет первообразную.
3. Если  - какая-нибудь первообразная непрерывной на отрезке
- какая-нибудь первообразная непрерывной на отрезке  функции
функции 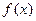 , то справедливо равенство
, то справедливо равенство
 ,
,
называемое формулой Ньютона – Лейбница.
1.24).  . 1.25).
. 1.25). 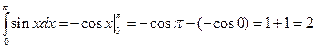 .
.
1.26).  .
.
Дата публикования: 2014-11-04; Прочитано: 258 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
